22-Suppose that X X, form a random sample from a beta distribution with parameters a and 8, where the value of a is known and the value of B is unknown (8> 0). The sufficient statistic for the parameter B is: log (h)
Equations and Inequations
Equations and inequalities describe the relationship between two mathematical expressions.
Linear Functions
A linear function can just be a constant, or it can be the constant multiplied with the variable like x or y. If the variables are of the form, x2, x1/2 or y2 it is not linear. The exponent over the variables should always be 1.
Solve it early I upvote

An estimate of a parameter θ is called a sufficient statistic if it contains all the information about θ contains in the sample. In other words, let T’ be any other estimate of θ and P(T,T’) be the joint probability density function (p.d.f) of T and T’ and let P(T’/T) be the conditional p.d.f of T’ given T. If P(T’/T) is independent of θ for all T’ then we say that T is a sufficient estimate of θ.
Let X1,………,Xn be a sample from a population with p.d.f. f(x, θ), then the joint p.d.f. of the sample usually called the likelihood of the sample is f(X1,………,Xn).
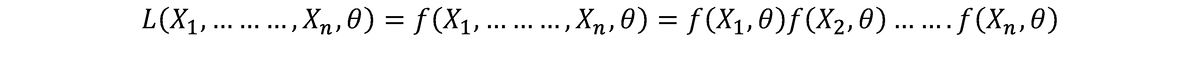
T is a sufficient estimate of θ if and only if it is possible to write

where L1(T, θ) is a function of T and θ alone and L2 is independent of θ.
Step by step
Solved in 2 steps with 9 images




