22 . A basketballwich con be modeled os a thin. 05 apherico shell, has cadius of 0.15m. If the boaste tball is Slling without sliding accoss a shell, hos a moss of 0250 ko amd a hodzontal loor at 4.25 mis Soetermine d(ross He Roto tional hrine tic Pinergy fthe bostet ball-
The moment of inertia of a thin spherical shell is given by
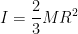
Where M = Mass of the shell, R = Radius of the shell
The rotational kinetic energy of the object is given by
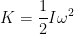
Where I = Moment of inertia,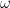 
= angular velocity of the shell
For rolling object without slipping
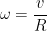
Where v = translational speed of the object
The mass of the basketball is M = 0.250 kg
The radius of the basketball is R = 0.15 m
The translational speed of the basketball is v = 4.25 m/s
The moment of inertia of the basketball is given by
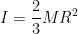...............(1)
The angular velocity of the basketball is given by
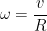...............(2)
The rotational kinetic energy of the basketball is given by
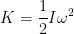
Using equation (1) and (2)
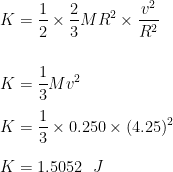
Step by step
Solved in 3 steps with 8 images
