Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
21. y" - 2y + 5y = e* cos(2x).

21. y" - 2y + 5y = e* cos(2x).

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
Question

Solve by variation of parameters

**Equation 21:** \[ y'' - 2y' + 5y = e^x \cos(2x) \] This is a second-order linear differential equation with constant coefficients and an exponential trigonometric forcing function. The left-hand side represents a homogeneous linear differential equation, while the right-hand side represents the non-homogeneous part, involving the product of an exponential function and a trigonometric function. Solving this type of equation typically involves finding the complementary (homogeneous) solution and particular (non-homogeneous) solution.
Transcribed Image Text:**Equation 21:** \[ y'' - 2y' + 5y = e^x \cos(2x) \] This is a second-order linear differential equation with constant coefficients and an exponential trigonometric forcing function. The left-hand side represents a homogeneous linear differential equation, while the right-hand side represents the non-homogeneous part, involving the product of an exponential function and a trigonometric function. Solving this type of equation typically involves finding the complementary (homogeneous) solution and particular (non-homogeneous) solution.
Expert Solution
Step 1: Useful formula

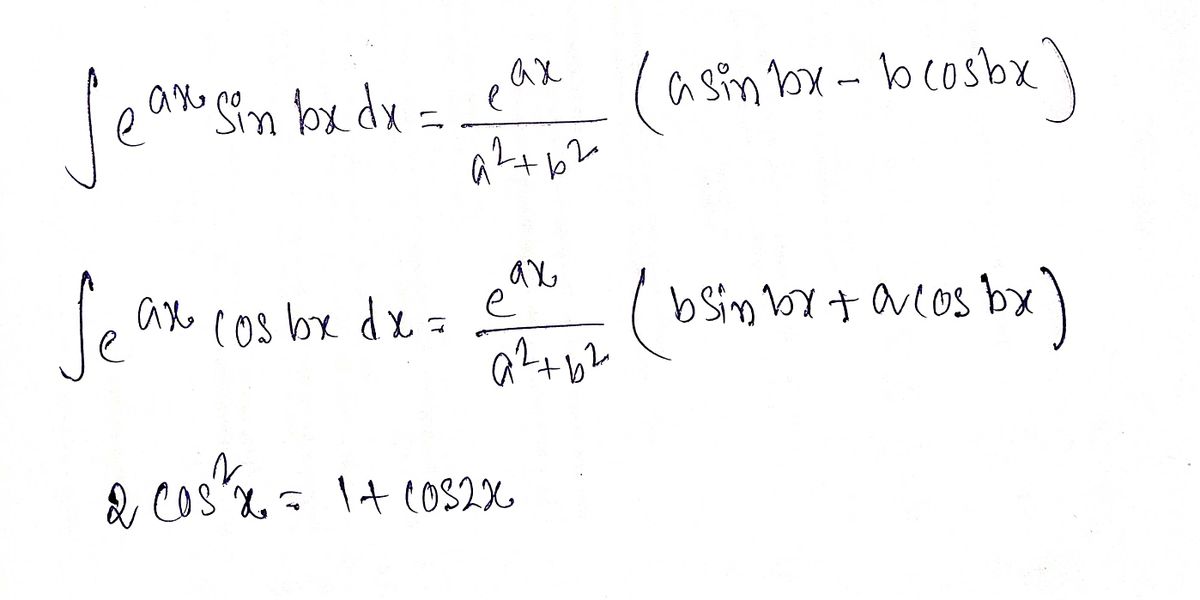
Advanced Math homework question answer, step 1, image 1

steps

Step by step

Solved in 5 steps with 5 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS