→ 21. Let T: R³ R³ be the linear transformation that re- flects each vector through the plane x₂ = 0. That is, T(X₁, X2, X3) = (x₁,-X2, x3). Find the standard matrix of T. 25
→ 21. Let T: R³ R³ be the linear transformation that re- flects each vector through the plane x₂ = 0. That is, T(X₁, X2, X3) = (x₁,-X2, x3). Find the standard matrix of T. 25
Algebra and Trigonometry (6th Edition)
6th Edition
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:Robert F. Blitzer
ChapterP: Prerequisites: Fundamental Concepts Of Algebra
Section: Chapter Questions
Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...
Related questions
Question
21
![19. Suppose V₁, V2, V3 are distinct points on one line in R³. The
line need not pass through the origin. Show that {V₁, V2, V3}
is linearly dependent.
20. Let T: R" → R" be a linear transformation, and suppose
T(u) = v. Show that T(-u) = -v.
->>>
21. Let T: R³ R³ be the linear transformation that re-
flects each vector through the plane x₂ = 0. That is,
T(X₁, X₂, X3) = (x₁, x2, x3). Find the standard matrix of T.
22. Let A be a 3 x 3 matrix with the property that the linear
transformation x →→ Ax maps R³ onto R³. Explain why the
transformation must be one-to-one.
23. A Givens rotation is a linear transformation from R" to R"
used in computer programs to create a zero entry in a vector
(usually a column of a matrix). The standard matrix of a
Givens rotation in R2 has the form
a² + b² = 1
a -b
[86].
a
Find a and b such that
[3]
is rotated into
(4,3)
(5,0)
[5].
X₁
24
25.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fad941f7b-34e1-41bc-b27d-c60dbcd610a1%2Fd26a3a7c-d262-46a0-9fab-f7577d8cb266%2F0qbisx3_processed.jpeg&w=3840&q=75)
Transcribed Image Text:19. Suppose V₁, V2, V3 are distinct points on one line in R³. The
line need not pass through the origin. Show that {V₁, V2, V3}
is linearly dependent.
20. Let T: R" → R" be a linear transformation, and suppose
T(u) = v. Show that T(-u) = -v.
->>>
21. Let T: R³ R³ be the linear transformation that re-
flects each vector through the plane x₂ = 0. That is,
T(X₁, X₂, X3) = (x₁, x2, x3). Find the standard matrix of T.
22. Let A be a 3 x 3 matrix with the property that the linear
transformation x →→ Ax maps R³ onto R³. Explain why the
transformation must be one-to-one.
23. A Givens rotation is a linear transformation from R" to R"
used in computer programs to create a zero entry in a vector
(usually a column of a matrix). The standard matrix of a
Givens rotation in R2 has the form
a² + b² = 1
a -b
[86].
a
Find a and b such that
[3]
is rotated into
(4,3)
(5,0)
[5].
X₁
24
25.
Expert Solution
Step 1
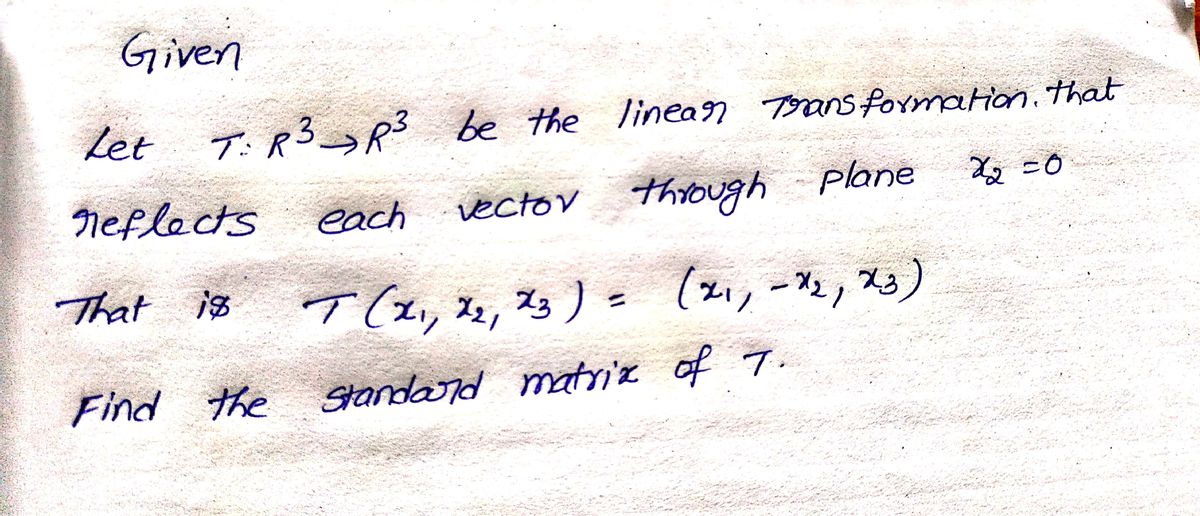
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:
9780135163078
Author:
Michael Sullivan
Publisher:
PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:
9780980232776
Author:
Gilbert Strang
Publisher:
Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:
9780077836344
Author:
Julie Miller, Donna Gerken
Publisher:
McGraw-Hill Education