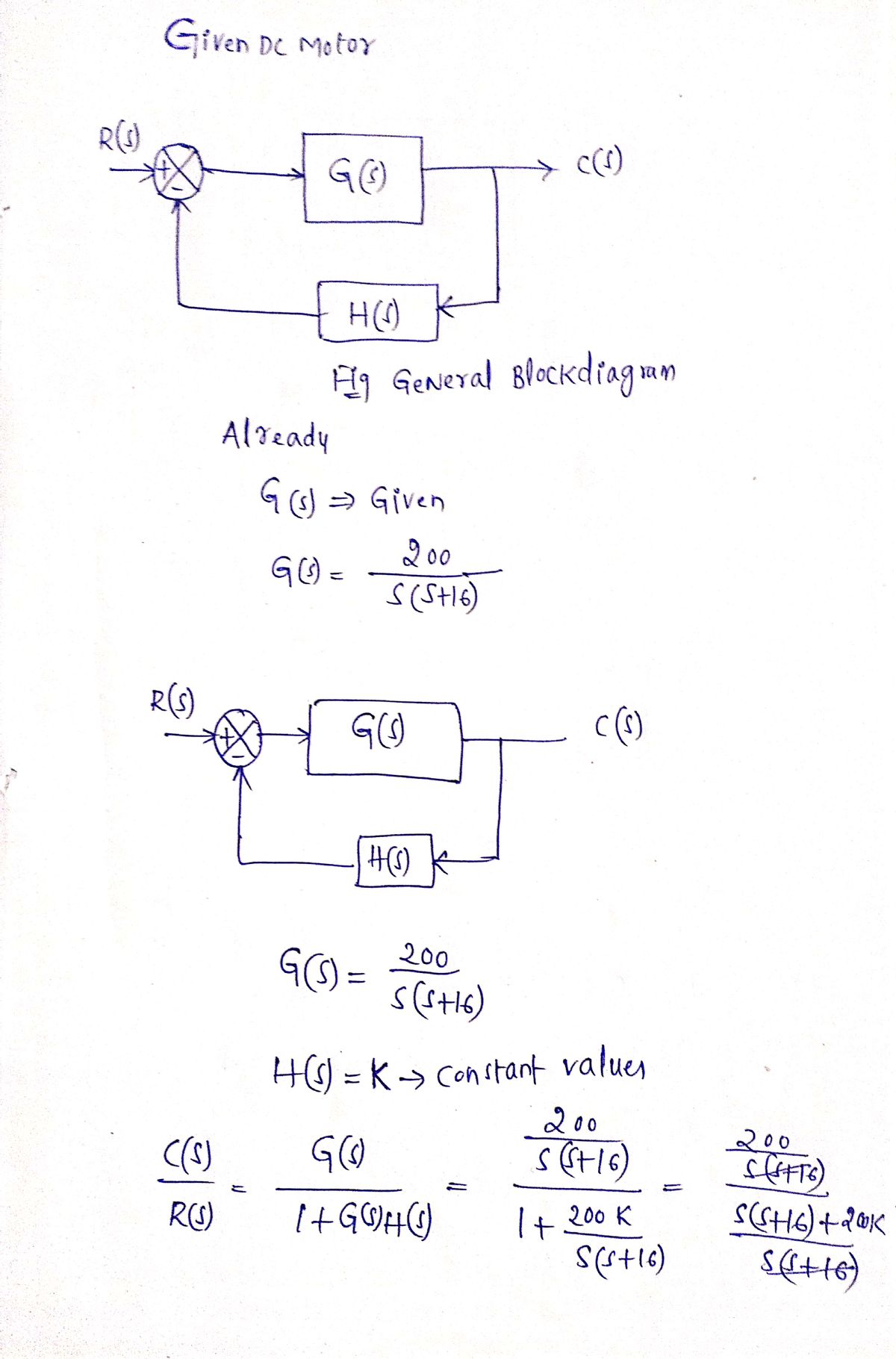
200 e(s) Y(S) S(S+16)
Transfer function
A transfer function (also known as system function or network function) of a system, subsystem, or component is a mathematical function that modifies the output of a system in each possible input. They are widely used in electronics and control systems.
Convolution Integral
Among all the electrical engineering students, this topic of convolution integral is very confusing. It is a mathematical operation of two functions f and g that produce another third type of function (f * g) , and this expresses how the shape of one is modified with the help of the other one. The process of computing it and the result function is known as convolution. After one is reversed and shifted, it is defined as the integral of the product of two functions. After producing the convolution function, the integral is evaluated for all the values of shift. The convolution integral has some similar features with the cross-correlation. The continuous or discrete variables for real-valued functions differ from cross-correlation (f * g) only by either of the two f(x) or g(x) is reflected about the y-axis or not. Therefore, it is a cross-correlation of f(x) and g(-x) or f(-x) and g(x), the cross-correlation operator is the adjoint of the operator of the convolution for complex-valued piecewise functions.
design a feedback control system which results in a closed system for the given DC motor that will be given below
Damping ratio is 0.6
natural frequency is 10 rad/sec
![The image shows a mathematical expression related to control systems, particularly a transfer function.
The transfer function is given by:
\[
\frac{\Theta(s)}{V_{in}(s)} = \frac{200}{s(s+16)}
\]
**Explanation:**
- \(\Theta(s)\) represents the output in the Laplace domain.
- \(V_{in}(s)\) represents the input in the Laplace domain.
- The equation shows how the output \(\Theta(s)\) relates to the input \(V_{in}(s)\) via the transfer function.
- The denominator \(s(s+16)\) suggests there are two poles in the system, one at the origin and another at \(s = -16\).
- The numerator \(200\) is the gain of the system.
This transfer function is useful for analyzing the dynamic behavior of systems and designing appropriate control strategies.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fdbb5604a-0a4b-46ed-92e3-55159cd22786%2F66be8ffe-90cf-46ab-a98e-d8950e0dee60%2F1wv6ff_processed.png&w=3840&q=75)
Step by step
Solved in 2 steps with 2 images









