2.5.11. Let 301= 20 = 0² be the common variance of √3X1 and 2 X2 and let p be the correlation coefficient of X₁ and X₂. Show for k> 0 that 5 P[|(X1-M1) + (X₂ - M₂)| ≥ ko] ≤ 6 + √√3 √2P k2
2.5.11. Let 301= 20 = 0² be the common variance of √3X1 and 2 X2 and let p be the correlation coefficient of X₁ and X₂. Show for k> 0 that 5 P[|(X1-M1) + (X₂ - M₂)| ≥ ko] ≤ 6 + √√3 √2P k2
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
Please only answer page 134 2.5.11
![n
S
Page 134,
2.5.11. Let 301 202 = 0² be the common variance of √3X1 and 2 X2 and let p be the
correlation coefficient of X₁ and X2. Show for k> 0 that
5
√2P
P[|(X1-M1) + (X2-H2)| ≥ko] ≤ 6 +
√3
k²](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fb54afed9-1b21-4ad6-9b4e-b2fef60f6136%2F6dd57bc1-8915-4aac-9d66-8c1ad9004933%2F1dsqtwi_processed.jpeg&w=3840&q=75)
Transcribed Image Text:n
S
Page 134,
2.5.11. Let 301 202 = 0² be the common variance of √3X1 and 2 X2 and let p be the
correlation coefficient of X₁ and X2. Show for k> 0 that
5
√2P
P[|(X1-M1) + (X2-H2)| ≥ko] ≤ 6 +
√3
k²
Expert Solution
Step 1
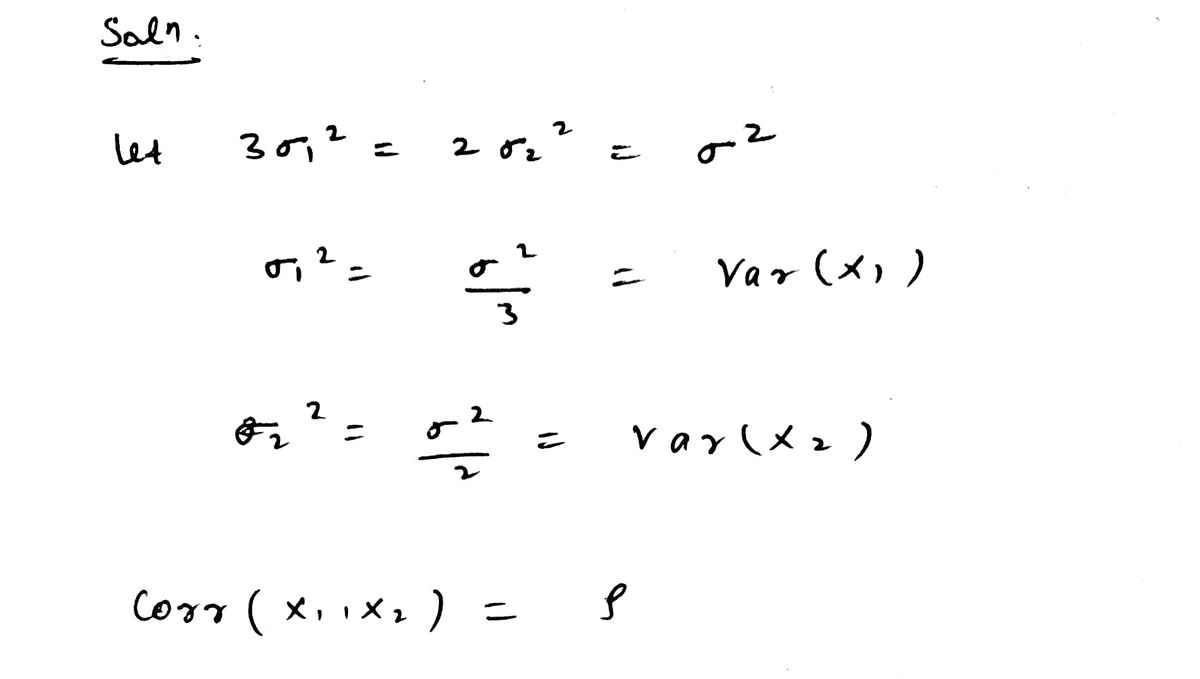
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
