#2 ### Understanding Quadratic Functions and Their GraphsIn this exercise, we will explore how the graph of \( y = ax^2 \) changes when the coefficient \( a \) is altered. We will observe how different values of \( a \), both positive and negative, influence the shape and direction of the parabola.#### Graphing Functions**1. 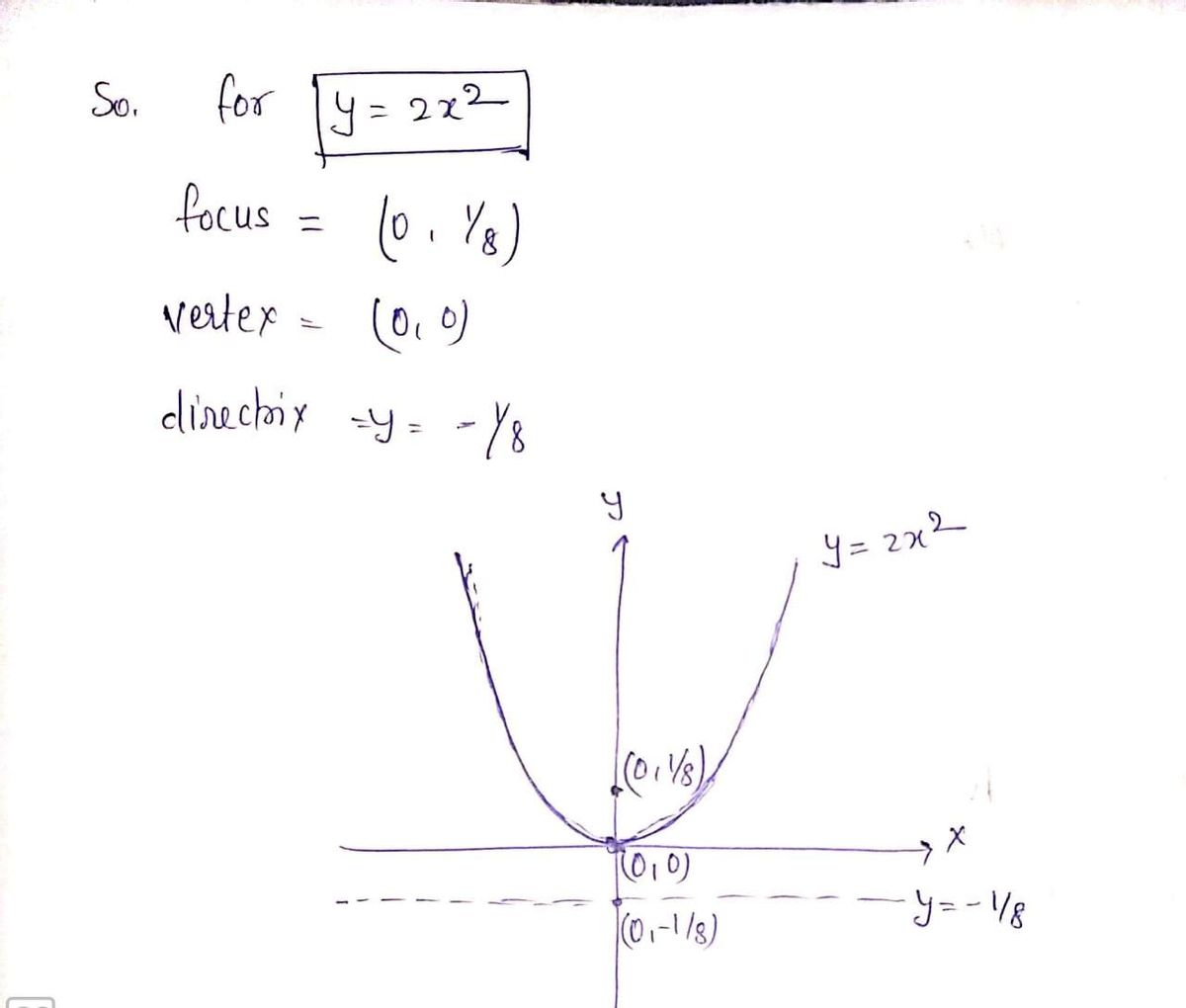\( y = x^2 \) and \( y = -x^2 \)**The first set of graphs involves \( y = x^2 \) and \( y = -x^2 \).- **Graph 1:** To be drawn on the provided grid showing a standard upward parabola for \( y = x^2 \) and a downward parabola for \( y = -x^2 \).**2. \( y = 2x^2 \) and \( y = -2x^2 \)**The second set of graphs involves \( y = 2x^2 \) and \( y = -2x^2 \).- **Graph 2:** To be drawn on the provided grid showing a narrower upward parabola for \( y = 2x^2 \) and a narrower downward parabola for \( y = -2x^2 \).**3. \( y = \frac{1}{2} x^2 \) and \( y = 3x^2 \)**The third set of graphs involves \( y = \frac{1}{2} x^2 \) and \( y = 3x^2 \).- **Graph 3:** To be drawn on the provided grid showing a wider upward parabola for \( y = \frac{1}{2} x^2 \) and a very narrow upward parabola for \( y = 3x^2 \).### Explanation of Graphs- **Graph 1:** Plots the functions \( y = x^2 \) and \( y = -x^2 \). The positive coefficient in \( y = x^2 \) results in a standard upward-opening parabola, while the negative coefficient in \( y = -x^2 \) flips the graph to open downward.- **Graph 2:** Plots the functions \( y = 2x^2 \) and \( y = -2x^2 \). The constant factor \( 2 \) causes both parabolas to be narrower than the par

Name: #2 ### Understanding Quadratic Functions and Their GraphsIn this exerc
Uploaded: 2024-03-20T07:06:41.000Z
Channel: Bartleby
Description: #2 ### Understanding Quadratic Functions and Their GraphsIn this exercise, we will explore how the graph of \( y = ax^2 \) changes when the coefficient \( a \) is altered. We will observe how different values of \( a \), both positive and negative, i