2. Use the definition of convex functions to answer the following: (a) Show that f: RdR given by f(x₁,...,₁)= ||||= Σ is convex. (b) Show that f: RR given by f(x) = |a| is convex. Hint: You may have to break up the argument into several cases around the sign of the inputs. (c) For (b), show that f is not strongly convex. (d) Show that f: R→ R given by f(x)=√ is not convex.
2. Use the definition of convex functions to answer the following: (a) Show that f: RdR given by f(x₁,...,₁)= ||||= Σ is convex. (b) Show that f: RR given by f(x) = |a| is convex. Hint: You may have to break up the argument into several cases around the sign of the inputs. (c) For (b), show that f is not strongly convex. (d) Show that f: R→ R given by f(x)=√ is not convex.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Q2

Transcribed Image Text:2. Use the definition of convex functions to answer the following:
(a) Show that f: RdR given by f(x₁,...,₁)= ||||= Σ
is convex.
(b) Show that f: RR given by f(x) = |a| is convex. Hint: You may have to
break up the argument into several cases around the sign of the inputs.
(c) For (b), show that f is not strongly convex.
(d) Show that f: R→ R given by f(x)=√ is not convex.
Expert Solution
Step 1
As per guidelines, I can do only first three subparts of the question.
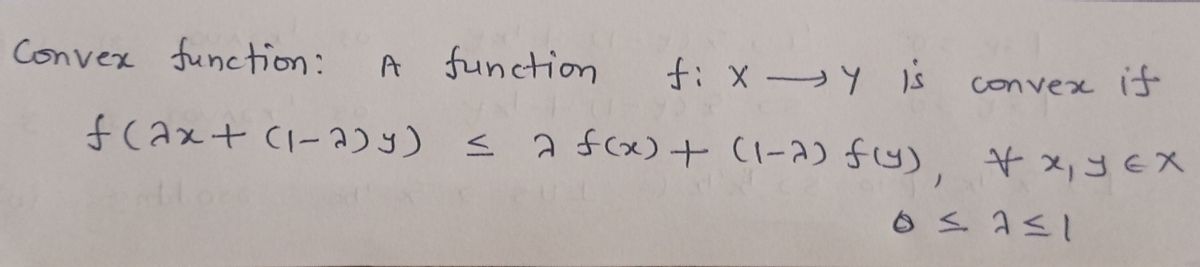
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

