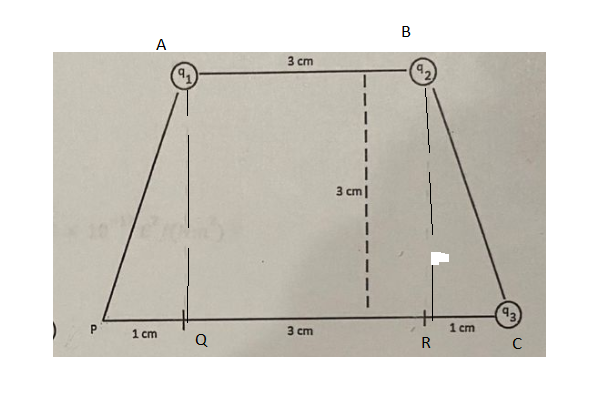
2. Three point charges are fixed in place at the corners of a trapezoid as shown. The upper side has length 3.0 cm, the base has length 5.0 cm and the height is 3.0 cm. q, =+ 10.0 nC, 3 cm =- 5.0 nC, and 93 =+ 5.0 nC. 92 a. Find the electric field at point P, the lower left corner of the trapezoid. b. Find the electric potential at point P taking the potential at infinity to be zero. 3 cm| -27 = 1. 67 x 10 "kg) 1 cm c. Suppose a proton (m is placed at point P and is released from rest. What will its speed be when it is very far from the arrangement of charges? 1 cm 3 cm

2. Three point charges are fixed in place at the corners of a trapezoid as shown. The upper side has length 3.0 cm, the base has length 5.0 cm and the height is 3.0 cm. q, =+ 10.0 nC, 3 cm =- 5.0 nC, and 93 =+ 5.0 nC. 92 a. Find the electric field at point P, the lower left corner of the trapezoid. b. Find the electric potential at point P taking the potential at infinity to be zero. 3 cm| -27 = 1. 67 x 10 "kg) 1 cm c. Suppose a proton (m is placed at point P and is released from rest. What will its speed be when it is very far from the arrangement of charges? 1 cm 3 cm