2. Show that each of the following graphs are not planar by finding a subgraph that is isomorphic to a subdivision of either K5 or K3,3. Be sure to label the vertices! (a) (b) (c) E D H 15. A E H 3 E D F G E B D B H
2. Show that each of the following graphs are not planar by finding a subgraph that is isomorphic to a subdivision of either K5 or K3,3. Be sure to label the vertices! (a) (b) (c) E D H 15. A E H 3 E D F G E B D B H
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:The image contains a problem statement and three graph diagrams labeled (a), (b), and (c).
---
**Problem Statement:**
2. Show that each of the following graphs are not planar by finding a subgraph that is isomorphic to a subdivision of either \( K_5 \) or \( K_{3,3} \). Be sure to label the vertices!
---
**Graph Diagrams:**
**(a) Graph Description:**
- This graph resembles a pentagon with additional internal connections.
- Vertices \( A, B, C, D, \) and \( E \) form the outer pentagon.
- Internal vertices are \( F, G, H, I, \) and \( J \).
- Edges are drawn such that:
- \( A \) is connected to \( F \) and \( B \).
- \( B \) is connected to \( G \) and \( C \).
- \( C \) is connected to \( H \) and \( D \).
- \( D \) is connected to \( I \) and \( E \).
- \( E \) is connected to \( J \) and \( A \).
- The internal vertices \( J, F, G, H, I \) form a star-like shape with additional internal connections, where \( F \) is connected to \( G, H, \) and \( I\), and each pair of \( G, H, I, J\) is interconnected.
**(b) Graph Description:**
- This graph is structured as a 10-sided polygon with interconnections.
- Outer vertices are \( A, B, C, D, E, F, G, H, I, \) and \( J \).
- Internal connections form a complete inner 5-sided network between \( G, I, J, H, \) and \( F \).
- Edges connect every alternate outer vertex:
- i.e., \( A \) to \( C \), \( B \) to \( D \), and so on.
**(c) Graph Description:**
- Shaped like a square inside a square.
- Outer vertices are \( A, B, G, \) and \( H \) forming a square.
- Inner vertices are \( C, D, E, \) and \( F \) forming another square.
- Diagonal edges cross, connecting:
- \(
Expert Solution
Step 1
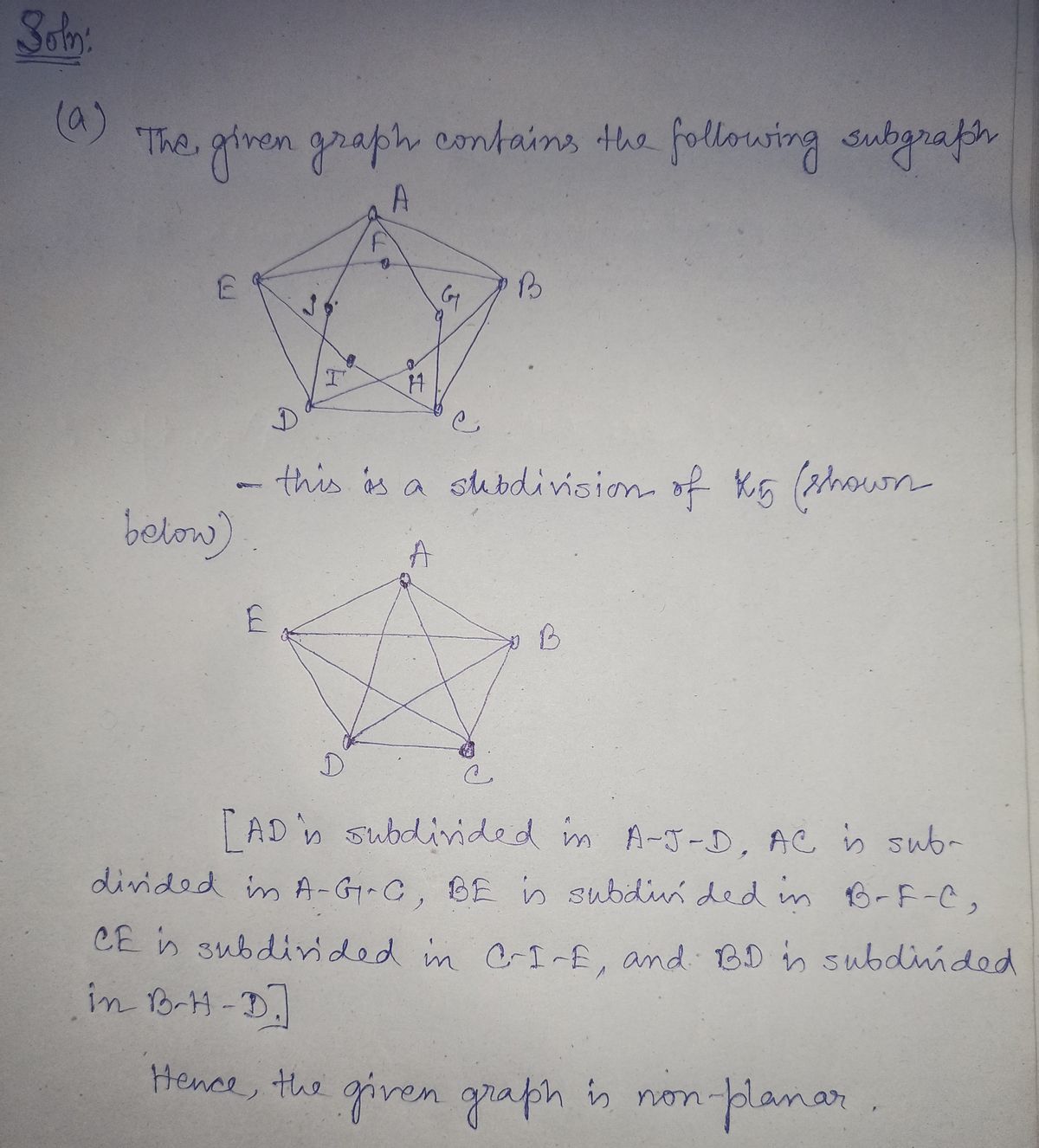
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

