2. Let T exp(1) be exponentially distributed random time with intensity > 0. Consider a continuous-time stochastic process {X}2o defined by X₁ = (a) Write down the state space S of X₁. (b) Show for u < s t. P(X₁ = 1|X, = 0, Xµ = 0) = P(X₂ = 1|X, = 0), and conclude whether or not X, is a Markov process. (c) To verify that X, is time homogeneous, show for s < t that P(X₂ = 1|X, = 0) = P(X₁-s 1|Xo = 0). (d) The corresponding intensity matrix Q of X, is defined by 900 901 Q: =( :). = 910 911 qij = lim t→0 where the off-diagonal element q¡j, j ‡ i, i, j ¤ {0, 1}, is given by P(X₂ = j|Xo = i) t Derive the intensity matrix of the Markov process X. (e) Find the transition probability matrix P(t) of X.
2. Let T exp(1) be exponentially distributed random time with intensity > 0. Consider a continuous-time stochastic process {X}2o defined by X₁ = (a) Write down the state space S of X₁. (b) Show for u < s t. P(X₁ = 1|X, = 0, Xµ = 0) = P(X₂ = 1|X, = 0), and conclude whether or not X, is a Markov process. (c) To verify that X, is time homogeneous, show for s < t that P(X₂ = 1|X, = 0) = P(X₁-s 1|Xo = 0). (d) The corresponding intensity matrix Q of X, is defined by 900 901 Q: =( :). = 910 911 qij = lim t→0 where the off-diagonal element q¡j, j ‡ i, i, j ¤ {0, 1}, is given by P(X₂ = j|Xo = i) t Derive the intensity matrix of the Markov process X. (e) Find the transition probability matrix P(t) of X.
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question
I need this question completed in 5 minutes with handwritten working

Transcribed Image Text:2. Let T exp(1) be exponentially distributed random time with intensity > 0. Consider a
continuous-time stochastic process {X}2o defined by
X₁
(a) Write down the state space S of X₁.
(b) Show for u < s < t that
=
1, T ≤t,
0,
T>t.
P(X₁ = 1|X, = 0, X₁ = 0) = P(X₂ = 1|X, = 0),
Xµ
and conclude whether or not X, is a Markov process.
(c) To verify that X, is time homogeneous, show for s < t that
P(X₂ = 1|X, = 0) = P(X-s = 1|Xo = 0).
(d) The corresponding intensity matrix Q of X, is defined by
e=(
qij
2010).
900 901
910 911
where the off-diagonal element qij, j ‡ i, i, j € {0, 1}, is given by
P(X₁ = j|Xo = i)
t
= lim
t→0
Derive the intensity matrix of the Markov process X.
(e) Find the transition probability matrix P(t) of X.
Expert Solution
Step 1: Determine the state space
(As per our standard guidelines, we are supposed to answer only 3 sub-parts.)
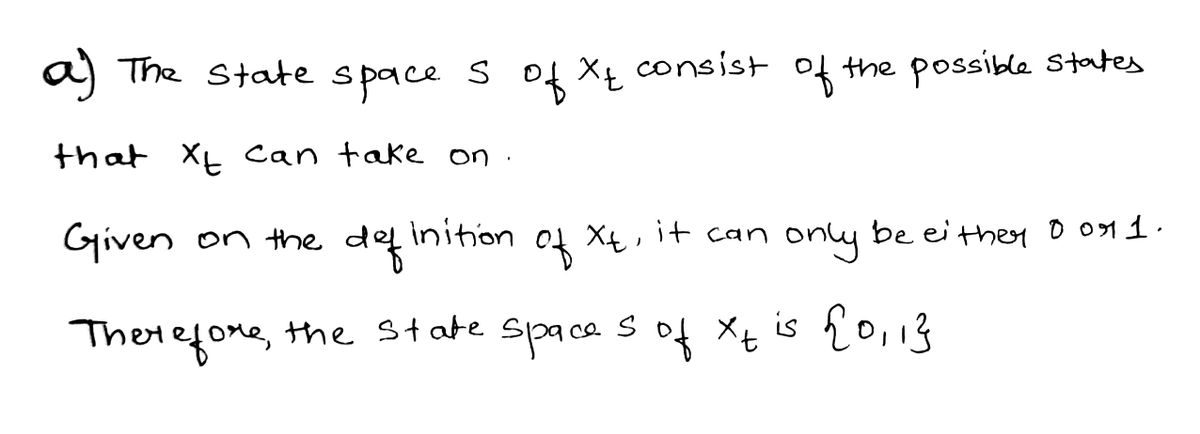
Step by step
Solved in 4 steps with 5 images

Recommended textbooks for you

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON

The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman