2. Consider an experiment of rolling five dice. (a) [1 (b) What is the probability that the five dice come up different values? s] What is the probability of obtaining two odd numbers and three even numbers?
2. Consider an experiment of rolling five dice. (a) [1 (b) What is the probability that the five dice come up different values? s] What is the probability of obtaining two odd numbers and three even numbers?
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
PLEAS HELP with this review.
#2
![2. Consider an experiment of rolling five dice.
(a) [1
(b)
What is the probability that the five dice come up different values?
What is the probability of obtaining two odd numbers and three even numbers?
3. In a bag, there are 8 blue marbles, 10 red marbles and 12 green marbles. When 4 marbles are
randomly chosen from the bag, find each of the following probabilities.
(a) [1
(b)
What is the probability that all chosen marbles have the same color?
] If it's known that none of the chosen marbles are green, what is the
probability of getting more blue marbles than red marbles?
4. Let A and B be events.
(a)
(b)
Assume P(A) = 0.57, P (B) = 0.78, and P(A n B) = 0.42. Find P(A U BC).
Assume P(A) = 0.57, P (B) = 0.78, and P(A | B) = 0.65. Find P(B|A).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fe8f98c03-2dea-45fe-9e7d-c001811b98bd%2F65eb8b66-1c1a-4185-ac63-a4c4739f4240%2Fa0h8xz8_processed.jpeg&w=3840&q=75)
Transcribed Image Text:2. Consider an experiment of rolling five dice.
(a) [1
(b)
What is the probability that the five dice come up different values?
What is the probability of obtaining two odd numbers and three even numbers?
3. In a bag, there are 8 blue marbles, 10 red marbles and 12 green marbles. When 4 marbles are
randomly chosen from the bag, find each of the following probabilities.
(a) [1
(b)
What is the probability that all chosen marbles have the same color?
] If it's known that none of the chosen marbles are green, what is the
probability of getting more blue marbles than red marbles?
4. Let A and B be events.
(a)
(b)
Assume P(A) = 0.57, P (B) = 0.78, and P(A n B) = 0.42. Find P(A U BC).
Assume P(A) = 0.57, P (B) = 0.78, and P(A | B) = 0.65. Find P(B|A).
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
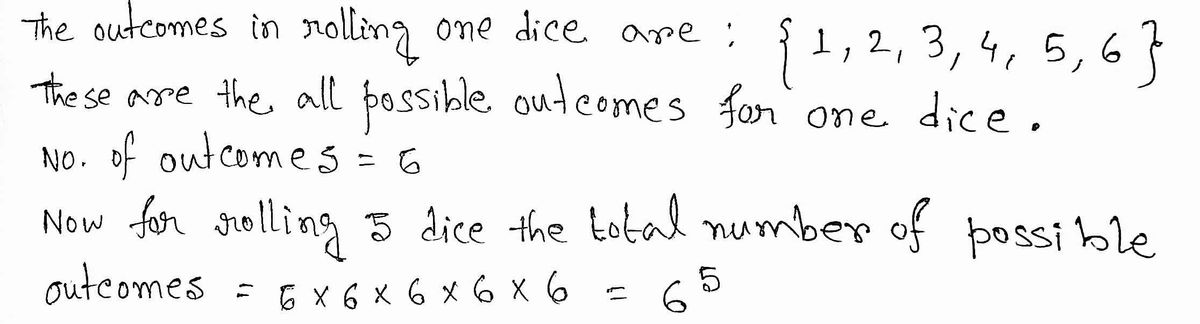
Step by step
Solved in 3 steps with 3 images
Recommended textbooks for you
A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON