Homework Help is Here – Start Your Trial Now!
Science
Advanced Physics
2) Rotations in 3D space, given by group SO(3), can be obtained by extending SO(2). For rotation in 3D space by angle through the z can be described by 3x3 orthogonal matrix R₂(9) = coso -sino 0 sing cosp 0 0 1 dRz Using the same procedure, find the generator S₂= −i Tp=0 do

2) Rotations in 3D space, given by group SO(3), can be obtained by extending SO(2). For rotation in 3D space by angle through the z can be described by 3x3 orthogonal matrix R₂(9) = coso -sino 0 sing cosp 0 0 1 dRz Using the same procedure, find the generator S₂= −i Tp=0 do

icon
Related questions
Question
100%

Thank you, can you do this with the this problem too? 

2) Rotations in 3D space, given by group SO(3), can be obtained by extending SO(2). For rotation in 3D space by angle through the z can be described by 3x3 orthogonal matrix R₂(9) = coso -sino 0 sing cosp 0 0 1 dRz Using the same procedure, find the generator S₂= −i Tp=0 do
Transcribed Image Text:2) Rotations in 3D space, given by group SO(3), can be obtained by extending SO(2). For rotation in 3D space by angle through the z can be described by 3x3 orthogonal matrix R₂(9) = coso -sino 0 sing cosp 0 0 1 dRz Using the same procedure, find the generator S₂= −i Tp=0 do
Expert Solution
steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question

How about this:

SO(2) can be extended for 3D rotation through the x-axis by an angle α. 

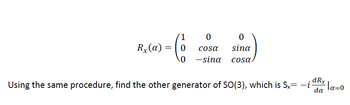
Rx (a) = 1 0 10 0 0 cosa sina -sina cosa. dRx da Using the same procedure, find the other generator of SO(3), which is Sx= —i ·la=0
Transcribed Image Text:Rx (a) = 1 0 10 0 0 cosa sina -sina cosa. dRx da Using the same procedure, find the other generator of SO(3), which is Sx= —i ·la=0
Solution
Bartleby Expert
SEE SOLUTION