(2) Let V₁ = V2 An Echelon form of (c) The linear system " [360 37 30 1 10 36 20 and V3 = Choose all of the true statements (there could be more than one): (d) If x₁v₁ + x₂V2 + x3V3 (a) The set {V₁, V2, V3} is linearly independent. (b) The set {V1, V2, V3} is linearly dependent. 360 37 3 1 2 1 362 = 3600 0130 0010 0 000 X1 X2 X3 861 has only one solution. 0, then at least one of x1, x2, or x3 are non-zero.
(2) Let V₁ = V2 An Echelon form of (c) The linear system " [360 37 30 1 10 36 20 and V3 = Choose all of the true statements (there could be more than one): (d) If x₁v₁ + x₂V2 + x3V3 (a) The set {V₁, V2, V3} is linearly independent. (b) The set {V1, V2, V3} is linearly dependent. 360 37 3 1 2 1 362 = 3600 0130 0010 0 000 X1 X2 X3 861 has only one solution. 0, then at least one of x1, x2, or x3 are non-zero.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

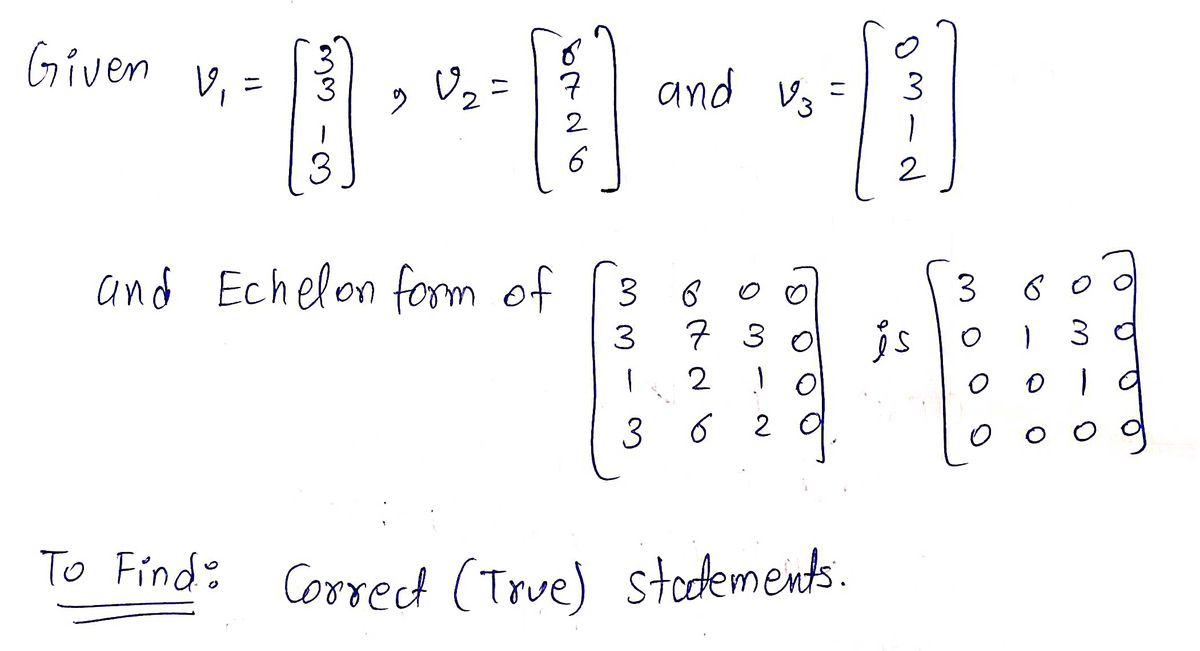
Transcribed Image Text:(2) Let \(\mathbf{v}_1 = \begin{bmatrix} 3 \\ 3 \\ 1 \\ 3 \end{bmatrix}\), \(\mathbf{v}_2 = \begin{bmatrix} 6 \\ 7 \\ 2 \\ 6 \end{bmatrix}\), and \(\mathbf{v}_3 = \begin{bmatrix} 0 \\ 3 \\ 1 \\ 2 \end{bmatrix}\).
An Echelon form of \(\begin{bmatrix} 3 & 6 & 0 & 0 \\ 3 & 7 & 3 & 0 \\ 1 & 2 & 1 & 0 \\ 3 & 6 & 2 & 0 \end{bmatrix}\) is \(\begin{bmatrix} 3 & 6 & 0 & 0 \\ 0 & 1 & 3 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}\).
Choose all of the true statements (there could be more than one):
(a) The set \(\{\mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3\}\) is linearly independent.
(b) The set \(\{\mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3\}\) is linearly dependent.
(c) The linear system \(\begin{bmatrix} 3 & 6 & 0 \\ 3 & 7 & 3 \\ 1 & 2 & 1 \\ 3 & 6 & 2 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}\) has only one solution.
(d) If \(x_1\mathbf{v}_1 + x_2\mathbf{v}_2 + x_3\mathbf{v}_3 = \mathbf{0}\), then at least one of \(x_1, x_2, x_3\) are non-zero.
Expert Solution
Step 1: Given
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

