Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question

Transcribed Image Text:### Problem Description
**Task:** Draw a graph of a continuous function that satisfies the following conditions:
1. \( f'(4) > 0 \)
2. \( f'(-6) < 0 \)
3. \( f''(2) < 0 \)
4. \( f(-1) = 3 \)
### Explanation of the Graph
#### Axes and Scale
- The graph is drawn on a standard Cartesian coordinate system.
- The x-axis is labeled and marked with integers ranging from -8 to 8.
- The y-axis extends both upwards and downwards from the origin.
#### Conditions Explained
1. **\( f'(4) > 0 \):** The slope of the function at \( x = 4 \) is positive. This implies the graph is increasing at this point.
2. **\( f'(-6) < 0 \):** The slope of the function at \( x = -6 \) is negative. This implies the graph is decreasing at this point.
3. **\( f''(2) < 0 \):** The second derivative at \( x = 2 \) is negative, indicating that the graph is concave down at this point.
4. **\( f(-1) = 3 \):** The value of the function at \( x = -1 \) is 3. This means that the point \((-1, 3)\) lies on the graph.
This exercise involves interpreting and sketching a graph based on derivative conditions, showcasing how the first and second derivatives affect the shape of the function.
Expert Solution
Step 1
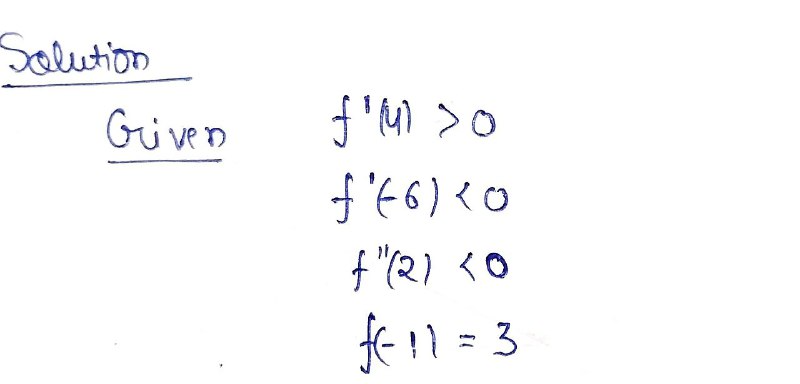
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning