Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
Please help solve this calculus question about critical points and extreme values:
Picture attached be
![### Local Maximums on \([-3, 3]\)
#### Instructions
Using the graph of \(h(x)\), identify all the values of \(c\) for which \(h(c)\) is a local maximum of the function \(h\).
#### Graph Explanation
- The graph displayed is of the function \(y = h(x)\).
- The x-axis ranges from -3 to 3, and the y-axis ranges from -2 to 3.
- The function exhibits several peaks and troughs, indicating local maximums and minimums.
**Key Observations:**
- A local maximum appears to occur at \(x \approx -1.5\) with the function value slightly above 0.
- Another local maximum is noted at \(x \approx 1\) where \(h(x)\) reaches its highest point on the graph, just above 2.
#### Interactive Component
- An input area is provided for entering the values of \(c\).
- Additional tools include options for uploading files, voice input, and mathematical symbols.
When you identify the local maximums, enter your findings in the provided text box and click “Submit” to check your answers.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ff5c5b462-e5a2-4c1c-9c45-1707b5796920%2F4bfa7176-f231-4d60-827f-7e106644873b%2F5p73kiy_processed.jpeg&w=3840&q=75)
Transcribed Image Text:### Local Maximums on \([-3, 3]\)
#### Instructions
Using the graph of \(h(x)\), identify all the values of \(c\) for which \(h(c)\) is a local maximum of the function \(h\).
#### Graph Explanation
- The graph displayed is of the function \(y = h(x)\).
- The x-axis ranges from -3 to 3, and the y-axis ranges from -2 to 3.
- The function exhibits several peaks and troughs, indicating local maximums and minimums.
**Key Observations:**
- A local maximum appears to occur at \(x \approx -1.5\) with the function value slightly above 0.
- Another local maximum is noted at \(x \approx 1\) where \(h(x)\) reaches its highest point on the graph, just above 2.
#### Interactive Component
- An input area is provided for entering the values of \(c\).
- Additional tools include options for uploading files, voice input, and mathematical symbols.
When you identify the local maximums, enter your findings in the provided text box and click “Submit” to check your answers.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 5 steps with 4 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Thank you, but I have one more question related to the previous question: I have attached a photo below
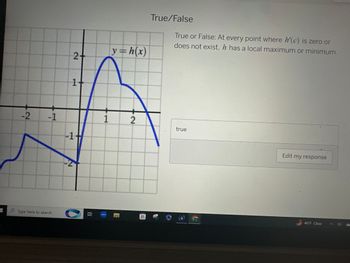
Transcribed Image Text:**True/False Question:**
Statement: At every point where \( h'(c) \) is zero or does not exist, \( h \) has a local maximum or minimum.
Response: true
**Graph Description:**
- The graph shows the function \( y = h(x) \).
- It features several curves and peaks.
- The x-axis ranges approximately from -3 to 3, and the y-axis ranges from -3 to 3.
- Notable features:
- A peak near \( x = 1 \) which indicates a local maximum.
- A local minimum occurs around \( x = 0 \).
- The graph demonstrates the behavior of \( h(x) \) at points where the derivative may be zero or undefined.
Solution
Follow-up Question
Hello, that was correct. But would it be possible if you can help with the rest of the question?
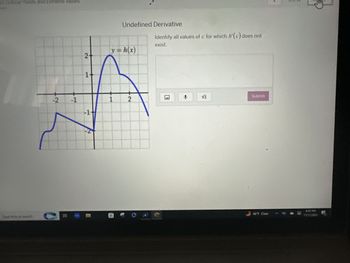
Transcribed Image Text:5 Critical Points and Extreme Values
Type here to search
-2
II
-1
2-
1
-1
-2
Undefined Derivative
y=h(x)
1
2
Identify all values of c for which h'(c) does not
exist.
VE
Submit
46°F Clear
OF TO
11/13/2023
Transcribed Image Text:-2
-1
2-
1.
-1
-2
1
y=h(x)
2
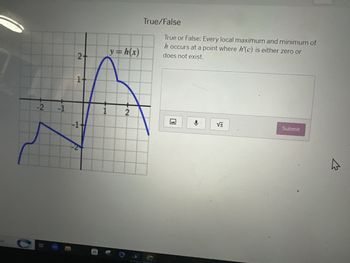
True/False
True or False: Every local maximum and minimum of
h occurs at a point where h'(c) is either zero or
does not exist.
❤
VE
Submit
4
Solution
Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning