Homework Help is Here – Start Your Trial Now!
Math
Calculus
Using the graph of h(x). identify all of the values of c for which h(c) is a local maximum of function h

Using the graph of h(x). identify all of the values of c for which h(c) is a local maximum of function h

Calculus: Early Transcendentals
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
See similar textbooks
icon
Related questions
Question

Please help solve this calculus question about critical points and extreme values:

Picture attached be

### Local Maximums on \([-3, 3]\) #### Instructions Using the graph of \(h(x)\), identify all the values of \(c\) for which \(h(c)\) is a local maximum of the function \(h\). #### Graph Explanation - The graph displayed is of the function \(y = h(x)\). - The x-axis ranges from -3 to 3, and the y-axis ranges from -2 to 3. - The function exhibits several peaks and troughs, indicating local maximums and minimums. **Key Observations:** - A local maximum appears to occur at \(x \approx -1.5\) with the function value slightly above 0. - Another local maximum is noted at \(x \approx 1\) where \(h(x)\) reaches its highest point on the graph, just above 2. #### Interactive Component - An input area is provided for entering the values of \(c\). - Additional tools include options for uploading files, voice input, and mathematical symbols. When you identify the local maximums, enter your findings in the provided text box and click “Submit” to check your answers.
Transcribed Image Text:### Local Maximums on \([-3, 3]\) #### Instructions Using the graph of \(h(x)\), identify all the values of \(c\) for which \(h(c)\) is a local maximum of the function \(h\). #### Graph Explanation - The graph displayed is of the function \(y = h(x)\). - The x-axis ranges from -3 to 3, and the y-axis ranges from -2 to 3. - The function exhibits several peaks and troughs, indicating local maximums and minimums. **Key Observations:** - A local maximum appears to occur at \(x \approx -1.5\) with the function value slightly above 0. - Another local maximum is noted at \(x \approx 1\) where \(h(x)\) reaches its highest point on the graph, just above 2. #### Interactive Component - An input area is provided for entering the values of \(c\). - Additional tools include options for uploading files, voice input, and mathematical symbols. When you identify the local maximums, enter your findings in the provided text box and click “Submit” to check your answers.
Expert Solution
steps

Step by step

Solved in 5 steps with 4 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question

Thank you, but I have one more question related to the previous question: I have attached a photo below 

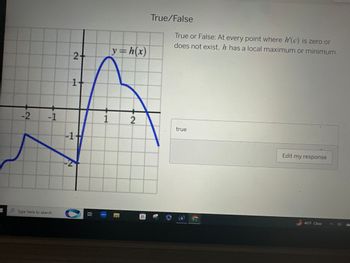
**True/False Question:** Statement: At every point where \( h'(c) \) is zero or does not exist, \( h \) has a local maximum or minimum. Response: true **Graph Description:** - The graph shows the function \( y = h(x) \). - It features several curves and peaks. - The x-axis ranges approximately from -3 to 3, and the y-axis ranges from -3 to 3. - Notable features: - A peak near \( x = 1 \) which indicates a local maximum. - A local minimum occurs around \( x = 0 \). - The graph demonstrates the behavior of \( h(x) \) at points where the derivative may be zero or undefined.
Transcribed Image Text:**True/False Question:** Statement: At every point where \( h'(c) \) is zero or does not exist, \( h \) has a local maximum or minimum. Response: true **Graph Description:** - The graph shows the function \( y = h(x) \). - It features several curves and peaks. - The x-axis ranges approximately from -3 to 3, and the y-axis ranges from -3 to 3. - Notable features: - A peak near \( x = 1 \) which indicates a local maximum. - A local minimum occurs around \( x = 0 \). - The graph demonstrates the behavior of \( h(x) \) at points where the derivative may be zero or undefined.
Solution
Bartleby Expert
SEE SOLUTION
Follow-up Question

Hello, that was correct. But would it be possible if you can help with the rest of the question? 

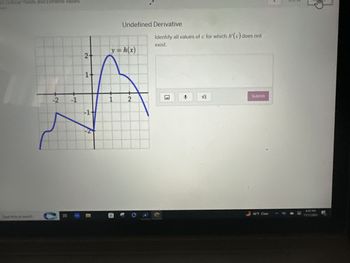
5 Critical Points and Extreme Values Type here to search -2 II -1 2- 1 -1 -2 Undefined Derivative y=h(x) 1 2 Identify all values of c for which h'(c) does not exist. VE Submit 46°F Clear OF TO 11/13/2023
Transcribed Image Text:5 Critical Points and Extreme Values Type here to search -2 II -1 2- 1 -1 -2 Undefined Derivative y=h(x) 1 2 Identify all values of c for which h'(c) does not exist. VE Submit 46°F Clear OF TO 11/13/2023
-2 -1 2- 1. -1 -2 1 y=h(x) 2 True/False True or False: Every local maximum and minimum of h occurs at a point where h'(c) is either zero or does not exist. ❤ VE Submit 4
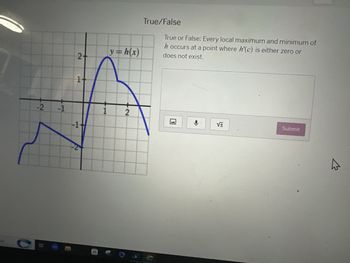
Transcribed Image Text:-2 -1 2- 1. -1 -2 1 y=h(x) 2 True/False True or False: Every local maximum and minimum of h occurs at a point where h'(c) is either zero or does not exist. ❤ VE Submit 4
Solution
Bartleby Expert
SEE SOLUTION
Recommended textbooks for you
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning
Thomas' Calculus (14th Edition)
Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman
Precalculus
Precalculus
Calculus
ISBN:
9780135189405
Author:
Michael Sullivan
Publisher:
PEARSON
Calculus: Early Transcendental Functions
Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning
SEE MORE TEXTBOOKS