Homework Help is Here – Start Your Trial Now!
Engineering
Mechanical Engineering
1a. Consider the problem 2-15 from Ozisik (1993). Starting with the heat diffusion equation, Eq. 1-11a in Ozisik (1993), show how it can be reduced to: Ꭷ2Ꭲ Ꭷ2Ꭲ + əx² əy² = 0 in [0 < x

1a. Consider the problem 2-15 from Ozisik (1993). Starting with the heat diffusion equation, Eq. 1-11a in Ozisik (1993), show how it can be reduced to: Ꭷ2Ꭲ Ꭷ2Ꭲ + əx² əy² = 0 in [0 < x

Elements Of Electromagnetics
Elements Of Electromagnetics
7th Edition
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Sadiku, Matthew N. O.
ChapterMA: Math Assessment
Section: Chapter Questions
Problem 1.1MA
See similar textbooks
icon
Related questions
Question

This question Has multiple parts, i need just the Part B solved, Part A is about driving the equation that is mentioned in part a, Use that equation and the table to solve part b, should be simple.

1a. Consider the problem 2-15 from Ozisik (1993). Starting with the heat diffusion equation, Eq. 1-11a in Ozisik (1993), show how it can be reduced to: a²T ²T + = 0 əx² əy² in [0<x<a; 0<y<b], subjected to the following boundary conditions: ƏT ƏT = 0 at x = 0; +HT = 0 at x = a; ax əx T = f(x) at y = 0; ƏT + HT = 0 at y = b ду All assumptions must be clearly stated and justified, and all steps clearly explained. 1b. Using separation of variables, show how the eigenfunction from Table 2-2 in Ozisik (1993) was derived. X(Pm, x) = cospmx Each step of your formulation must be clearly explained, and all assumptions justified.
Transcribed Image Text:1a. Consider the problem 2-15 from Ozisik (1993). Starting with the heat diffusion equation, Eq. 1-11a in Ozisik (1993), show how it can be reduced to: a²T ²T + = 0 əx² əy² in [0<x<a; 0<y<b], subjected to the following boundary conditions: ƏT ƏT = 0 at x = 0; +HT = 0 at x = a; ax əx T = f(x) at y = 0; ƏT + HT = 0 at y = b ду All assumptions must be clearly stated and justified, and all steps clearly explained. 1b. Using separation of variables, show how the eigenfunction from Table 2-2 in Ozisik (1993) was derived. X(Pm, x) = cospmx Each step of your formulation must be clearly explained, and all assumptions justified.
5 6 TABLE 2-2 The Solution X(), the Norm NB) and the Eigenvalues of the Differential Equation Subject to the Boundary Conditions Shown in the Table Below Boundary Condition at x=0 No. 1 2 7 3 4 dX -=+H₁X=0 dx 9 - dX dx dx dX dx dX ö dX -=0 X=0 X=0 + H₂X=0 +H₁X=0 dX dx dx dX i X=0. dX dx A dX dx dX Boundary Condition at x = L dx +H₂X=0 = 0 X=0 d²X(x) dx² + H₂X=0 0 + H₂X=0 =0 +8²x(x)=0 in Bcos B+H, sin f cos B (L-x) X(Bmx) sin B (L-x) cos Bmx *cos Bmx cos x sin x sin ßx 0 < x <L X=0 sin Bmx X = 0 "For this particular case Bo-0 is also an eigenvalue corresponding to X = 1. 2 [10² + H²) (L 2- B²+H} L(B²+ H²) + H₂ 0 B²+ H₂ 2. LB² + H²) + H₂ 2 1/N(B) 8² + H² 2 L(B²+ H₂) + H₂ 2 L+ for for 8,0 NIJ B² + H² L(B²+ H₂) + H₂ 2 L H₂ ² + H² + H₁ Eigenvalues 's are Positive Roots of tan BL- _B_(H₁ + H₂) B²-H₂H₂ Plan BL=H₁ Bm cot BML=H₁ Pm tan PL=H₂ sin BL=0ª cos BL=0 Bm cot BmL=-H₂ cos BL=0 sin AL=0
Transcribed Image Text:5 6 TABLE 2-2 The Solution X(), the Norm NB) and the Eigenvalues of the Differential Equation Subject to the Boundary Conditions Shown in the Table Below Boundary Condition at x=0 No. 1 2 7 3 4 dX -=+H₁X=0 dx 9 - dX dx dx dX dx dX ö dX -=0 X=0 X=0 + H₂X=0 +H₁X=0 dX dx dx dX i X=0. dX dx A dX dx dX Boundary Condition at x = L dx +H₂X=0 = 0 X=0 d²X(x) dx² + H₂X=0 0 + H₂X=0 =0 +8²x(x)=0 in Bcos B+H, sin f cos B (L-x) X(Bmx) sin B (L-x) cos Bmx *cos Bmx cos x sin x sin ßx 0 < x <L X=0 sin Bmx X = 0 "For this particular case Bo-0 is also an eigenvalue corresponding to X = 1. 2 [10² + H²) (L 2- B²+H} L(B²+ H²) + H₂ 0 B²+ H₂ 2. LB² + H²) + H₂ 2 1/N(B) 8² + H² 2 L(B²+ H₂) + H₂ 2 L+ for for 8,0 NIJ B² + H² L(B²+ H₂) + H₂ 2 L H₂ ² + H² + H₁ Eigenvalues 's are Positive Roots of tan BL- _B_(H₁ + H₂) B²-H₂H₂ Plan BL=H₁ Bm cot BML=H₁ Pm tan PL=H₂ sin BL=0ª cos BL=0 Bm cot BmL=-H₂ cos BL=0 sin AL=0
Expert Solution
Step 1: Given data

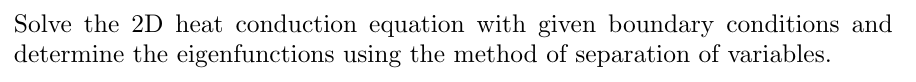
Mechanical Engineering homework question answer, step 1, image 1

steps

Step by step

Solved in 3 steps with 5 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Knowledge Booster
Atomic Diffusion in Solids
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.
Recommended textbooks for you
Elements Of Electromagnetics
Elements Of Electromagnetics
Mechanical Engineering
ISBN:
9780190698614
Author:
Sadiku, Matthew N. O.
Publisher:
Oxford University Press
Mechanics of Materials (10th Edition)
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:
9780134319650
Author:
Russell C. Hibbeler
Publisher:
PEARSON
Thermodynamics: An Engineering Approach
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:
9781259822674
Author:
Yunus A. Cengel Dr., Michael A. Boles
Publisher:
McGraw-Hill Education
Control Systems Engineering
Control Systems Engineering
Mechanical Engineering
ISBN:
9781118170519
Author:
Norman S. Nise
Publisher:
WILEY
Mechanics of Materials (MindTap Course List)
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:
9781337093347
Author:
Barry J. Goodno, James M. Gere
Publisher:
Cengage Learning
Engineering Mechanics: Statics
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:
9781118807330
Author:
James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:
WILEY
SEE MORE TEXTBOOKS