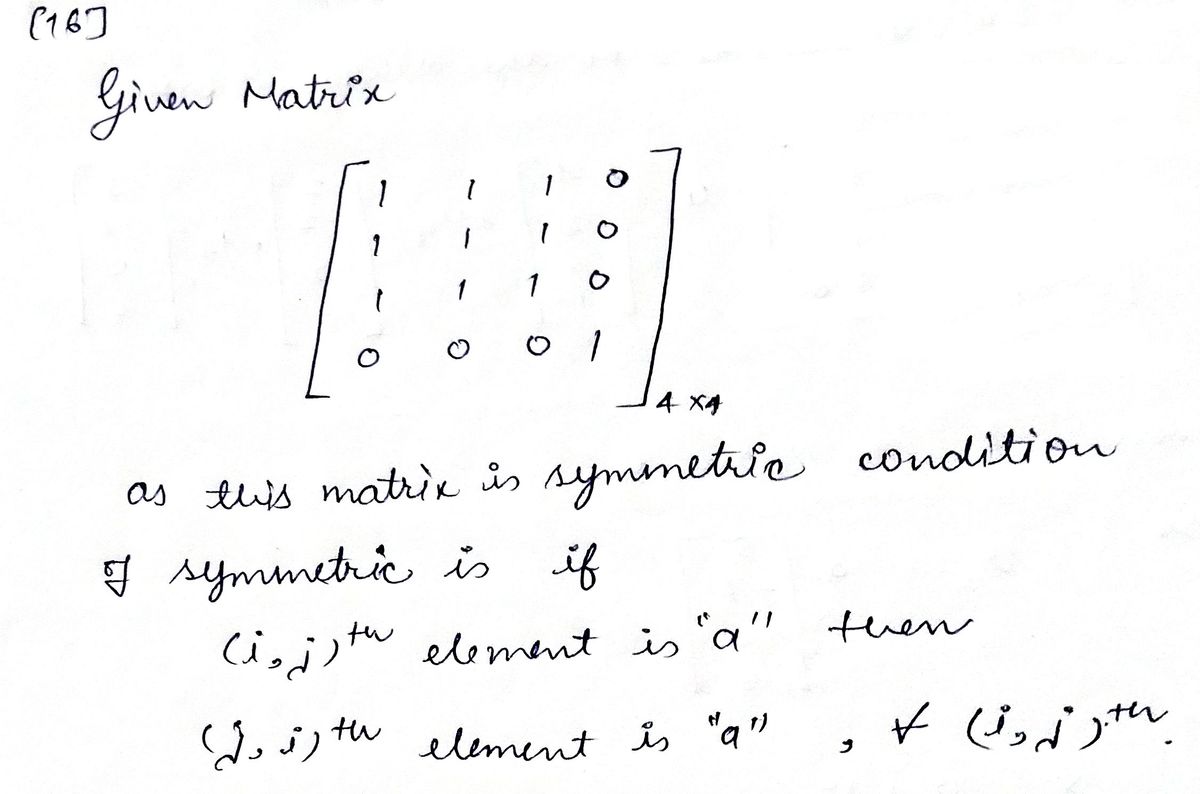
16 Required information NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. 1 1 1 0 1 1 1 0 1 1 10 0001 Consider the following zero-one matrix representing a relation on the ordered set (a, b, c, d). Identify the correct statement about the symmetric property of the relation represented by the given matrix. (You must provide an answer before moving to the next part.) Multiple Choice The (.th element is 1 whenever the (ith element is O. So, the relation is symmetric. The relation is not symmetric, because all the diagonal elements are 1s. The U, th element is 1 whenever the (.th element is 1. So, the relation is symmetric. The relation is symmetric, because all the diagonal elements are 1s.
16 Required information NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. 1 1 1 0 1 1 1 0 1 1 10 0001 Consider the following zero-one matrix representing a relation on the ordered set (a, b, c, d). Identify the correct statement about the symmetric property of the relation represented by the given matrix. (You must provide an answer before moving to the next part.) Multiple Choice The (.th element is 1 whenever the (ith element is O. So, the relation is symmetric. The relation is not symmetric, because all the diagonal elements are 1s. The U, th element is 1 whenever the (.th element is 1. So, the relation is symmetric. The relation is symmetric, because all the diagonal elements are 1s.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
100%
![**Question 16**
**Required Information**
*NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part.*
Consider the following zero-one matrix:
\[
\begin{bmatrix}
1 & 1 & 1 & 0 \\
1 & 1 & 1 & 0 \\
1 & 1 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\]
This matrix represents a relation on the ordered set \( \{a, b, c, d\} \).
Identify the correct statement about the symmetric property of the relation represented by the given matrix.
*(You must provide an answer before moving to the next part.)*
**Multiple Choice**
- ( ) The \((j, i)^{\text{th}}\) element is 1 whenever the \((i, j)^{\text{th}}\) element is 0. So, the relation is symmetric.
- ( ) The relation is not symmetric, because all the diagonal elements are 1s.
- ( ) The \((j, i)^{\text{th}}\) element is 1 whenever the \((i, j)^{\text{th}}\) element is 1. So, the relation is symmetric.
- ( ) The relation is symmetric, because all the diagonal elements are 1s.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F0405dc91-666b-4d31-b943-06bf4fafc05b%2F31862838-6b9f-4e37-8395-c9088496ce58%2Fn60enj_processed.png&w=3840&q=75)
Transcribed Image Text:**Question 16**
**Required Information**
*NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part.*
Consider the following zero-one matrix:
\[
\begin{bmatrix}
1 & 1 & 1 & 0 \\
1 & 1 & 1 & 0 \\
1 & 1 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\]
This matrix represents a relation on the ordered set \( \{a, b, c, d\} \).
Identify the correct statement about the symmetric property of the relation represented by the given matrix.
*(You must provide an answer before moving to the next part.)*
**Multiple Choice**
- ( ) The \((j, i)^{\text{th}}\) element is 1 whenever the \((i, j)^{\text{th}}\) element is 0. So, the relation is symmetric.
- ( ) The relation is not symmetric, because all the diagonal elements are 1s.
- ( ) The \((j, i)^{\text{th}}\) element is 1 whenever the \((i, j)^{\text{th}}\) element is 1. So, the relation is symmetric.
- ( ) The relation is symmetric, because all the diagonal elements are 1s.
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

