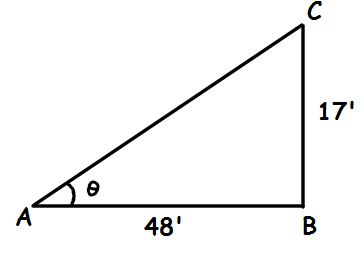
15. You are standing 48 horizontally from the base of a vertical wall 17' tall. What is the angle of elevation (in degrees) from your feet to the top of that wall?
15. You are standing 48 horizontally from the base of a vertical wall 17' tall. What is the angle of elevation (in degrees) from your feet to the top of that wall?
Trigonometry (11th Edition)
11th Edition
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Chapter1: Trigonometric Functions
Section: Chapter Questions
Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Related questions
Question
100%
![**Problem 15:**
You are standing 48' horizontally from the base of a vertical wall 17' tall. What is the angle of elevation (in degrees) from your feet to the top of that wall?
---
*Explanation:*
This problem involves finding the angle of elevation from a point on the ground to the top of a wall, given the horizontal distance from the wall and the height of the wall. This can be solved using trigonometric ratios, specifically the tangent function, since the problem describes a right triangle scenario.
- **Horizontal distance (adjacent side)**: 48 feet
- **Wall height (opposite side)**: 17 feet
To find the angle of elevation, use the formula:
\[
\text{tan}(\theta) = \frac{\text{opposite}}{\text{adjacent}}
\]
Substitute the given values:
\[
\text{tan}(\theta) = \frac{17}{48}
\]
Then, solve for \(\theta\) using the inverse tangent function:
\[
\theta = \text{tan}^{-1}\left(\frac{17}{48}\right)
\]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F2816e768-d46c-42f8-b287-986238abcd2a%2F587fbe98-3af3-43b2-8762-c11b67cb237f%2Fspaz8ji_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem 15:**
You are standing 48' horizontally from the base of a vertical wall 17' tall. What is the angle of elevation (in degrees) from your feet to the top of that wall?
---
*Explanation:*
This problem involves finding the angle of elevation from a point on the ground to the top of a wall, given the horizontal distance from the wall and the height of the wall. This can be solved using trigonometric ratios, specifically the tangent function, since the problem describes a right triangle scenario.
- **Horizontal distance (adjacent side)**: 48 feet
- **Wall height (opposite side)**: 17 feet
To find the angle of elevation, use the formula:
\[
\text{tan}(\theta) = \frac{\text{opposite}}{\text{adjacent}}
\]
Substitute the given values:
\[
\text{tan}(\theta) = \frac{17}{48}
\]
Then, solve for \(\theta\) using the inverse tangent function:
\[
\theta = \text{tan}^{-1}\left(\frac{17}{48}\right)
\]
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning