Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
11) find the derivative of the function.
![**Title: Understanding Functions in Algebra**
**Date: January 10, 2022**
In this session, we explore a mathematical function defined as follows:
\[ f(x) = 4x - 7\sqrt{x} + e^{x+2} \]
### Key Components of the Function
1. **Linear Term (4x):**
- This term represents a linear relationship between the input variable \(x\) and the output of the function. It suggests a direct proportion where the function increases steadily as \(x\) increases.
2. **Square Root Term (-7√x):**
- The square root function introduces a non-linear component. The coefficient (-7) indicates that as \(x\) increases, this term reduces the overall value of \(f(x)\) by an amount that grows in relation to the square root of \(x\).
3. **Exponential Term (e^{x+2}):**
- The exponential function, denoted by the constant e raised to the power of \(x+2\), plays a significant role in the behavior of the function. This term implies rapid growth, as exponential functions increase more quickly compared to linear or quadratic functions.
This equation combines multiple mathematical concepts, providing a rich basis for study in the context of algebra and calculus. It is an excellent example of how complex relationships can be expressed and explored through mathematical functions.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fb034729f-db63-4235-9b33-79c3c77be50a%2F2bf7a334-0fa1-460c-b500-9a6532fa6295%2F3zv2vkm_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Title: Understanding Functions in Algebra**
**Date: January 10, 2022**
In this session, we explore a mathematical function defined as follows:
\[ f(x) = 4x - 7\sqrt{x} + e^{x+2} \]
### Key Components of the Function
1. **Linear Term (4x):**
- This term represents a linear relationship between the input variable \(x\) and the output of the function. It suggests a direct proportion where the function increases steadily as \(x\) increases.
2. **Square Root Term (-7√x):**
- The square root function introduces a non-linear component. The coefficient (-7) indicates that as \(x\) increases, this term reduces the overall value of \(f(x)\) by an amount that grows in relation to the square root of \(x\).
3. **Exponential Term (e^{x+2}):**
- The exponential function, denoted by the constant e raised to the power of \(x+2\), plays a significant role in the behavior of the function. This term implies rapid growth, as exponential functions increase more quickly compared to linear or quadratic functions.
This equation combines multiple mathematical concepts, providing a rich basis for study in the context of algebra and calculus. It is an excellent example of how complex relationships can be expressed and explored through mathematical functions.
Expert Solution
Step 1
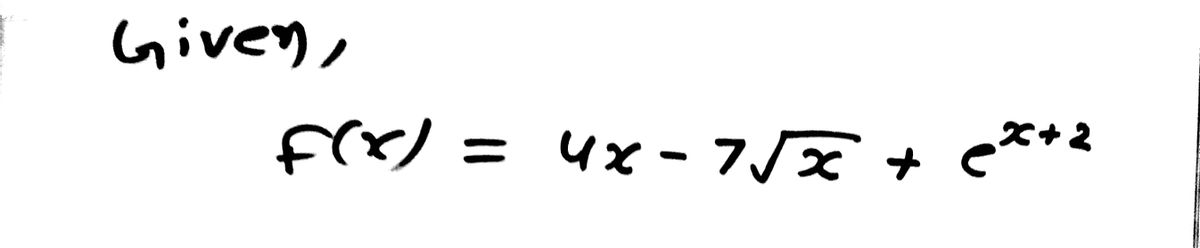
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning