108. (2 109. (-1 + i)6 15
Trigonometry (11th Edition)
11th Edition
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Chapter1: Trigonometric Functions
Section: Chapter Questions
Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Related questions
Question
Question 109
![**Finding a Power of a Complex Number**
In Exercises 107–126, use DeMoivre’s Theorem to find the indicated power of the complex number. Write the result in standard form.
107. \((1 + i)^3\)
108. \((2 + 2i)^6\)
109. \((-1 + i)^6\)
110. \((3 - 3i)^8\)
111. \(2(\sqrt{3} - i)^{5}\)
112. \(4(1 - \sqrt{3}i)^3\)
113. \([5(\cos 140^\circ + i \sin 140^\circ)]^{13}\)
114. \([3(\cos 150^\circ + i \sin 150^\circ)]^{4}\)
115. \(\left( \cos \frac{5\pi}{4} + i \sin \frac{5\pi}{4} \right)^{10}\)
116. \(2\left( \cos \frac{\pi}{2} + i \sin \frac{\pi}{2} \right)^{12}\)
117. \([2(\cos \pi + i \sin \pi)]^{14}\)
118. \((\cos 0 + i \sin 0)^{20}\)
119. \([4(\cos 10^\circ + i \sin 10^\circ)]^{6}\)
120. \([6(\cos 15^\circ + i \sin 15^\circ)]^{4}\)
121. \([3(\cos \frac{\pi}{8} + i \sin \frac{\pi}{8})]^{12}\)
Use DeMoivre’s Theorem, \((r(\cos \theta + i \sin \theta))^n = r^n (\cos(n\theta) + i \sin(n\theta))\), for calculating powers of complex numbers in polar form and convert the result to standard form \(a + bi\).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F085e24e4-6db3-44bd-bedd-407e7fcd33ea%2F432ce196-b6e5-4740-b02f-78f0665fbac9%2F7meox2s_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Finding a Power of a Complex Number**
In Exercises 107–126, use DeMoivre’s Theorem to find the indicated power of the complex number. Write the result in standard form.
107. \((1 + i)^3\)
108. \((2 + 2i)^6\)
109. \((-1 + i)^6\)
110. \((3 - 3i)^8\)
111. \(2(\sqrt{3} - i)^{5}\)
112. \(4(1 - \sqrt{3}i)^3\)
113. \([5(\cos 140^\circ + i \sin 140^\circ)]^{13}\)
114. \([3(\cos 150^\circ + i \sin 150^\circ)]^{4}\)
115. \(\left( \cos \frac{5\pi}{4} + i \sin \frac{5\pi}{4} \right)^{10}\)
116. \(2\left( \cos \frac{\pi}{2} + i \sin \frac{\pi}{2} \right)^{12}\)
117. \([2(\cos \pi + i \sin \pi)]^{14}\)
118. \((\cos 0 + i \sin 0)^{20}\)
119. \([4(\cos 10^\circ + i \sin 10^\circ)]^{6}\)
120. \([6(\cos 15^\circ + i \sin 15^\circ)]^{4}\)
121. \([3(\cos \frac{\pi}{8} + i \sin \frac{\pi}{8})]^{12}\)
Use DeMoivre’s Theorem, \((r(\cos \theta + i \sin \theta))^n = r^n (\cos(n\theta) + i \sin(n\theta))\), for calculating powers of complex numbers in polar form and convert the result to standard form \(a + bi\).
Expert Solution
Step 1
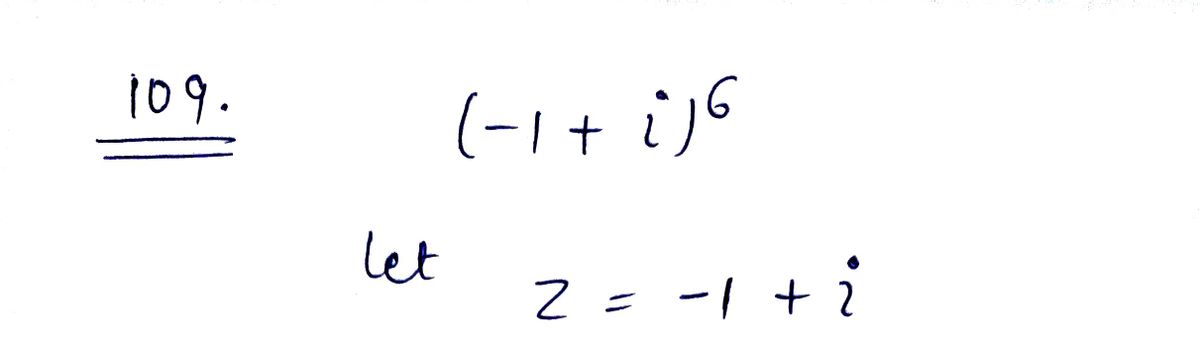
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning