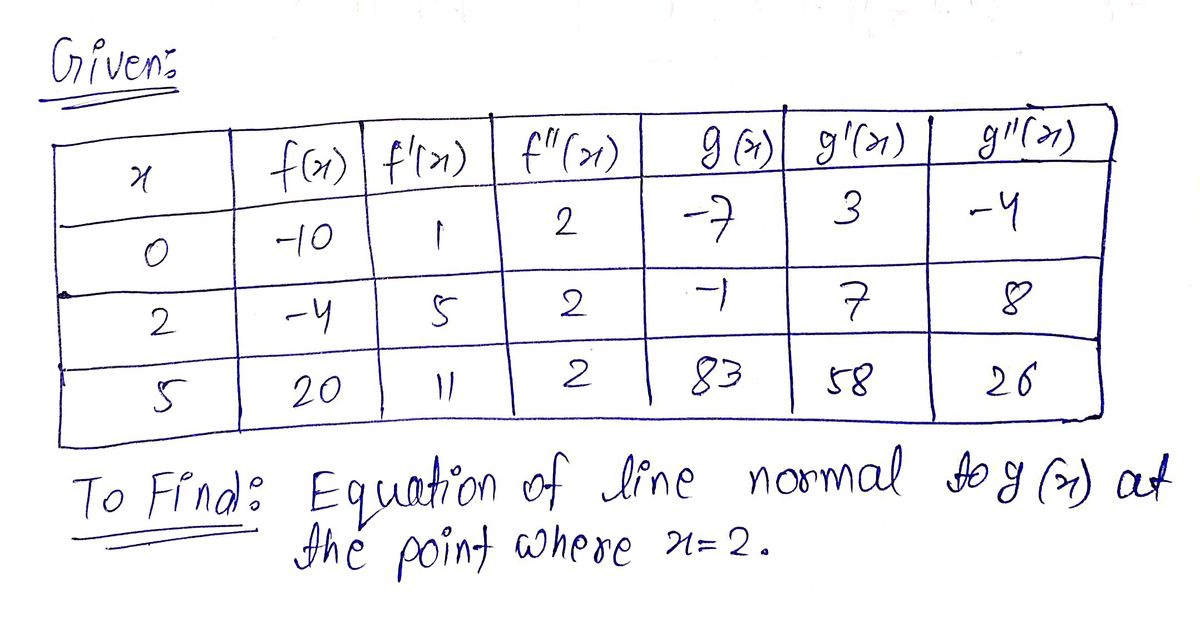
1025 f(x) -10 -4 20 f'(x) 1 5 11 f" (x) 2 2 2 g(x) -7 -1 83 g'(x) 3 7 58 g"(x) -4 8 26
1025 f(x) -10 -4 20 f'(x) 1 5 11 f" (x) 2 2 2 g(x) -7 -1 83 g'(x) 3 7 58 g"(x) -4 8 26
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Transcription:**
Write the equation of the line normal to g(x) at the point where x = 2.
---
**Explanation (for educational website):**
To find the equation of the line normal to the function \( g(x) \) at a specific point where \( x = 2 \), you should follow these steps:
1. **Find the Derivative**: Determine \( g'(x) \), the derivative of the function. This will give you the slope of the tangent line at any point \( x \).
2. **Evaluate the Derivative at \( x = 2 \)**: Calculate \( g'(2) \) to find the slope of the tangent line at this point.
3. **Find the Slope of the Normal Line**: The slope of the normal line is the negative reciprocal of the slope of the tangent line. So, if the slope of the tangent line is \( m \), the slope of the normal line is \( -1/m \).
4. **Determine the Y-Coordinate**: Find the y-coordinate of the point on the curve where \( x = 2 \) by evaluating \( g(2) \).
5. **Write the Equation of the Normal Line**: Use the point-slope form of the equation of a line:
\[
y - y_1 = m_{\text{normal}}(x - x_1)
\]
where \( (x_1, y_1) \) is the point \((2, g(2))\), and \( m_{\text{normal}} \) is the slope of the normal line.
By following these steps, you can successfully determine the equation of the normal line at \( x = 2 \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fc0da95ed-4961-453b-bb3e-75b23e1037ca%2Ff179f387-838c-4267-bf46-32dfc6cd32b0%2Ffglb70g_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Transcription:**
Write the equation of the line normal to g(x) at the point where x = 2.
---
**Explanation (for educational website):**
To find the equation of the line normal to the function \( g(x) \) at a specific point where \( x = 2 \), you should follow these steps:
1. **Find the Derivative**: Determine \( g'(x) \), the derivative of the function. This will give you the slope of the tangent line at any point \( x \).
2. **Evaluate the Derivative at \( x = 2 \)**: Calculate \( g'(2) \) to find the slope of the tangent line at this point.
3. **Find the Slope of the Normal Line**: The slope of the normal line is the negative reciprocal of the slope of the tangent line. So, if the slope of the tangent line is \( m \), the slope of the normal line is \( -1/m \).
4. **Determine the Y-Coordinate**: Find the y-coordinate of the point on the curve where \( x = 2 \) by evaluating \( g(2) \).
5. **Write the Equation of the Normal Line**: Use the point-slope form of the equation of a line:
\[
y - y_1 = m_{\text{normal}}(x - x_1)
\]
where \( (x_1, y_1) \) is the point \((2, g(2))\), and \( m_{\text{normal}} \) is the slope of the normal line.
By following these steps, you can successfully determine the equation of the normal line at \( x = 2 \).

Transcribed Image Text:The table below provides values of the functions \( f(x) \) and \( g(x) \), along with their first and second derivatives, at different values of \( x \).
| \( x \) | \( f(x) \) | \( f'(x) \) | \( f''(x) \) | \( g(x) \) | \( g'(x) \) | \( g''(x) \) |
|---------|-----------|-------------|-------------|-----------|-------------|-------------|
| 0 | -10 | 1 | 2 | -7 | 3 | -4 |
| 2 | -4 | 5 | 2 | -1 | 7 | 8 |
| 5 | 20 | 11 | 2 | 83 | 58 | 26 |
### Explanation
- **\( x \)**: The independent variable or input value.
- **\( f(x) \)**: The output of function \( f \) for each \( x \).
- **\( f'(x) \)**: The first derivative of \( f \), representing the rate of change of \( f \) at each \( x \).
- **\( f''(x) \)**: The second derivative of \( f \), indicating the curvature or the change of the rate of change of \( f \) at each \( x \).
- **\( g(x) \)**: The output of function \( g \) for each \( x \).
- **\( g'(x) \)**: The first derivative of \( g \), representing the rate of change of \( g \) at each \( x \).
- **\( g''(x) \)**: The second derivative of \( g \), indicating the curvature or the change of the rate of change of \( g \) at each \( x \).
Expert Solution
Step 1: Given;
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

