10 in 5) Find the centroid ( â, ŷ ) and Ix for the shape shown. Use a large rectangle and a small negative rectangle (which should have negative area and negative I, ) and the origin a shown. 4 in 6 in 10 in 15.5 in /6.5 in 1 5 in
Find the centroid (ˆˆ,xy) and Ix for the shape shown. Use a large rectangle and a small negative rectangle (which should have negative area and negative xI) and the origin a shown.
If the shape in problem 5 is used for a beam with Mmax = 25 k-ft, what is the maximum bending stress?

Solution:
Let large rectangle area A1=10×15.5=155in2
Let small rectangle area A2=6.5×6=39in2
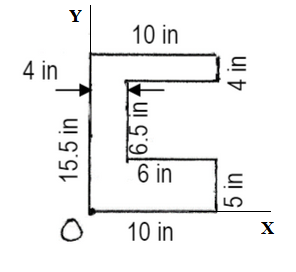
We need to find the position of centroid x' and y' from the x-axis and y-axis shown in above figure.
To find x-coordinate of the centroid
x-coordinate of centroid of area A1 (x1)=
x-coordinate of centroid of area A2 (x2)=
Then position of x-coordinate of the centroid of the section is given by,
To find y-coordinate of the centroid
y-coordinate of centroid of area A1 (y1)=
y-coordinate of centroid of area A2 (y2)=
Then position of y-coordinate of the centroid of the section is given by,
The position of centroid is (4.327,7.581)
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images









