(10) Find Std(X) when X is a discrete random variable with the following given density. (i) f(z) = , z = 6, 7, 8, 9, 10, (iii) f(x) = T,7 = 1,2, · . · , n, where n = 100, (9() (4) (vii) f(z) = 0.3(0.7)* , z = 0, 1, · .., (ix) f(x) = TD, z = 1, 2, - . . (v) f(x) = -, z = 0,1,2, 3,
(10) Find Std(X) when X is a discrete random variable with the following given density. (i) f(z) = , z = 6, 7, 8, 9, 10, (iii) f(x) = T,7 = 1,2, · . · , n, where n = 100, (9() (4) (vii) f(z) = 0.3(0.7)* , z = 0, 1, · .., (ix) f(x) = TD, z = 1, 2, - . . (v) f(x) = -, z = 0,1,2, 3,
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
Answer last two sub parts of Q. 10.
Note: This is one question with two sub parts

Transcribed Image Text:The image displays two multiple-choice questions, each with a set of possible answers.
### Question (vii)
The options for this question are displayed in a horizontal line with corresponding radio buttons:
- Option 1: \( \sqrt{7/3} \)
- Option 2: \( 0.7/\sqrt{0.3} \)
- Option 3: \( \sqrt{0.7}/0.3 \)
- Option 4: \( 7/3 \)
- Option 5: "None of the above"
- Option 6: "N/A" (selected)
### Question (xi)
The options for this question are similarly displayed in a horizontal line with radio buttons:
- Option 1: "Does not exist"
- Option 2: 1
- Option 3: 2
- Option 4: 3
- Option 5: 4
- Option 6: "N/A" (selected)
Both questions have a yellow background, and the currently selected answers are indicated with a filled circle in the "N/A" options.

Transcribed Image Text:**Finding the Standard Deviation of a Discrete Random Variable**
*Problem 10: Find \( \text{Std}(X) \) when \( X \) is a discrete random variable with the following given density functions:*
(i) \( f(x) = \frac{1}{5}, \, x = 6, 7, 8, 9, 10. \)
(ii) \( f(x) = \frac{1}{100}, \, x = 1, 2, \ldots, n, \) where \( n = 100. \)
(iii) \( f(x) = \frac{1}{\binom{6}{3}} \binom{6}{x}, \, x = 0, 1, 2, 3. \)
(iv) \( f(x) = 0.3 (0.7)^x, \, x = 0, 1, \ldots \)
(v) \( f(x) = \frac{1}{x(x+1)}, \, x = 1, 2, \ldots \)
**Explanation:**
1. **Probability Mass Functions (PMFs)**:
- Each function \( f(x) \) represents a PMF of a discrete random variable \( X \).
- The functions cover different probabilities for \( X \) taking certain integer values.
2. **Standard Deviation**:
- The task is to calculate the standard deviation \( \text{Std}(X) \) for each random variable \( X \) using the given PMFs.
- This involves finding the expected value \( E(X) \) and the variance \( \text{Var}(X) \), with \( \text{Std}(X) = \sqrt{\text{Var}(X)} \).
3. **Combinations and Factorials in (iii)**:
- Explanation of combinations \( \binom{n}{k} \) is necessary, which denotes the number of ways to choose \( k \) items from \( n \) without regard to order.
4. **Geometric Distribution in (iv)**:
- The function \( 0.3 (0.7)^x \) corresponds to the PMF of a geometric distribution that models the number of trials until the first success, here with a probability of success \( 0.3 \).
5. **
Expert Solution
Step 1
Solution.
Dear students the parts are different statement based question ,so they are treated as different question,so I have provided solution to only the first mentioned part.
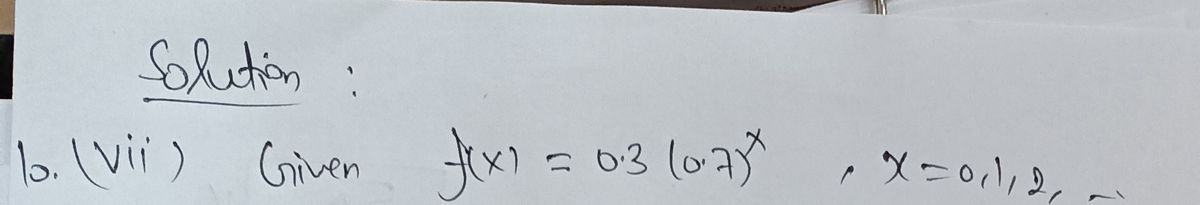
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
