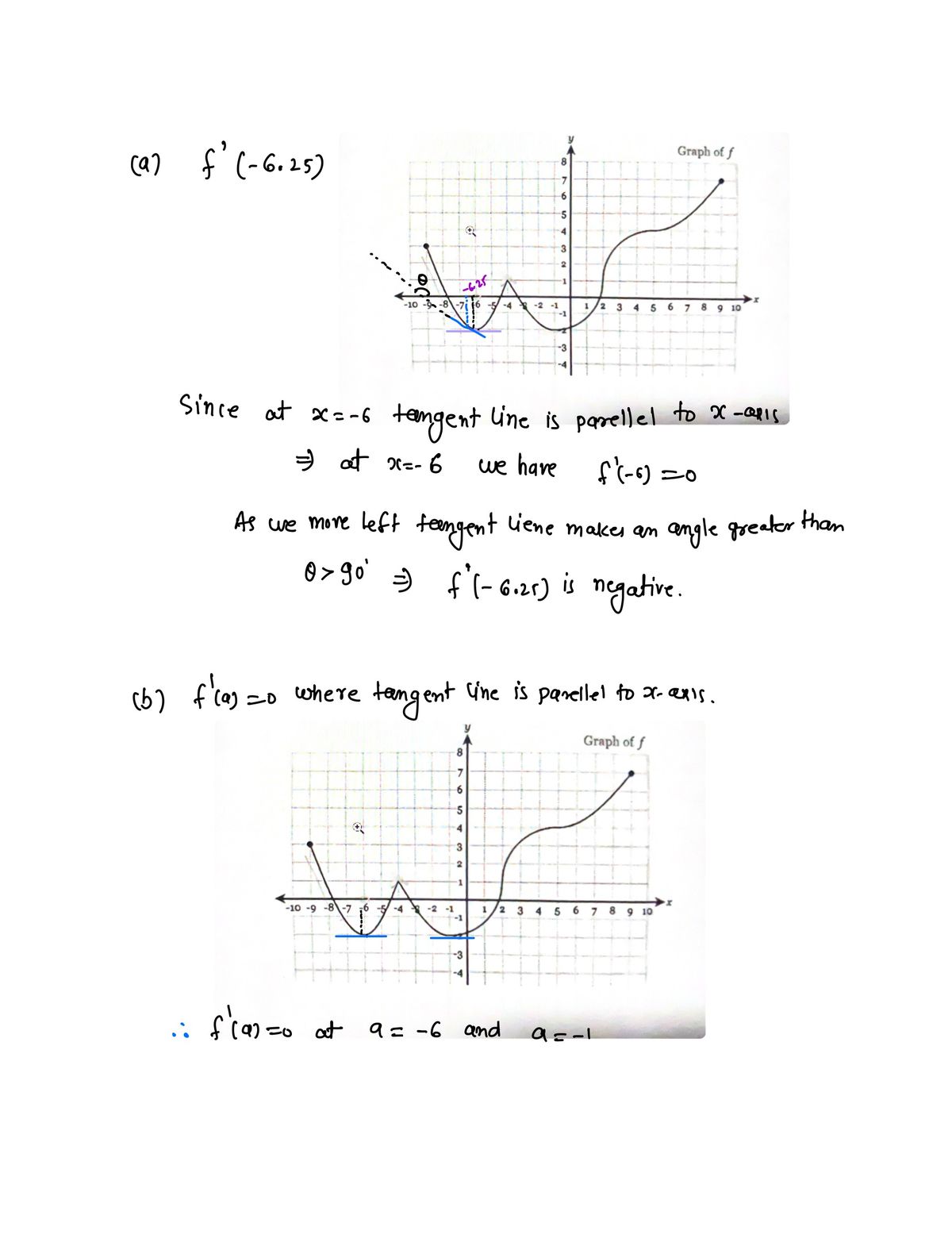
a) which statement best describes f'(-6.25)b) estimate the values of a for which f'(a) = 0C) give the intervals over which f is differentiable **Graph Description for Educational Website:**---The graph depicted is labeled as "Graph of \( f \)". It shows a continuous curve plotted on a coordinate plane with \( x \)-axis and \( y \)-axis, both ranging from -10 to 10 on the \( x \)-axis and from -4 to 8 on the \( y \)-axis.**Key Features of the Graph:**1. **Behavior on X-Axis:** - The curve starts at the upper left quadrant, approximately at (-10, 6), and decreases to intersect the x-axis between -9 and -8. - The curve reaches a minimum point around (-6, -2) before rising slightly and dipping again to touch the x-axis near (-4, 0).2. **Behavior Near Origin:** - The graph then peaks just under the origin, near the point (-2, 1), before decreasing again. - It swiftly climbs, crossing the x-axis at approximately (1, 0).3. **Positive Quadrant Movement:** - Moving into positive x-values, the curve ascends steadily, passing through points such as (3, 2) and curving upwards towards (6, 5). - It continues upwards, peaking around (9, 7.5).4. **General Observations:** - The curve displays characteristics of an oscillating wave-like pattern with multiple critical points. - It transitions smoothly through quadratic-like arches and linear segments, suggestive of a polynomial function.This graph can be used to analyze the behavior of the function \( f \), identify roots, turning points, and understand overall trends in the function’s behavior across the domain.

Answered: Image /qna-images/answer/682a8019-8332-4d7a-9021-d0f66d7bd092.jpg

Answered: -10 -9 -8-7 -6 -5 -4 8 -7 -6 -2 -1 5 4…

-10 -9 -8-7 -6 -5 -4 8 -7 -6 -2 -1 5 4 3 2 1 -1 -3 & 1 2 3 4 5 Graph of f 67 8 9 10

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

Similar questions

The line normal to the graph of f at the point (1,2) passes through the point (-1,1). Which of the following is the value of f'(1)? Be sure to explain your answer. A) -2B) 2C) -1/2D) 3
6. Consider the DERIVATIVE f' graphed below. Sketch a possible graph of the original function f on the provided coordinate plane. Clearly label the y-intercept of f' Graph of DERIVATIVE ƒ': Possible graph of f: 1 -4 -3 -2 1 1 3 1 -2 -3 –4
Find all extrema and any inflection points for the function f(x) = sec² x-2 tanx on the interval П П 63
The intervals for f’(x)
thank you!
Please show steps
Show your work please