1. State the following: a. State that “Properties of Absolute Values (b > 0)” b. State that “The Pythagorean Identities” c. State that “Horizontal Line Test” d. State that “The Law of Sines” e. State that “The Law of Cosines”
1. State the following:
a. State that “Properties of Absolute Values (b > 0)”
b. State that “The Pythagorean Identities”
c. State that “Horizontal Line Test”
d. State that “The Law of Sines”
e. State that “The Law of Cosines”
a. “Properties of Absolute Values (b > 0)”
- Non-negativity |a| ≥ 0
- Positive-definiteness |a| = 0a = 0
- Multiplicativity |ab| = |a| |b|
- Subadditivity |a + b| ≤ |a| + |b|
- Idempotence ||a|| = |a|
- Symmetry |−a| = |a|
- Identity of indiscernible |a − b| = 0 ⇔ a = b
- Triangle inequality |a − b| ≤ |a − c| + |c − b|
- Preservation of division |a/b|=|a|/|b| if b ≠ 0
b. “The Pythagorean Identities”
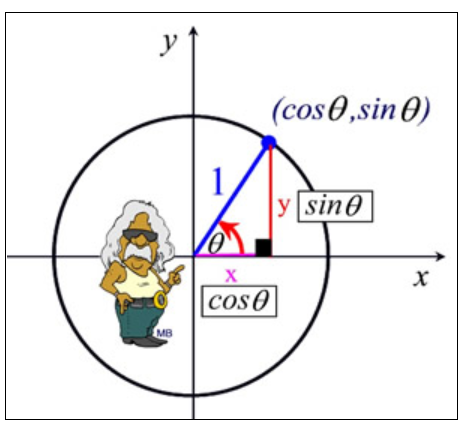
When studying the unit circle (radius of 1), it was observed that a point on the unit circle (a vertex of the right triangle) can be represented by the coordinates (cos θ, sin θ ).
Since the legs of the right triangle in the unit circle have the values of sin θ and cos θ, the Pythagorean Theorem can be used to obtain sin2 θ + cos2 θ = 1.
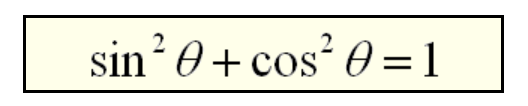
This well-known equation is called a Pythagorean Identity.
It is true for all values of θ in the unit circle.
Using this first Pythagorean Identity, two additional Pythagorean Identities can be created.

Step by step
Solved in 6 steps with 7 images









