1. Problem 6.1.8 A. 2. sin x В. sin x С. V3(sin x) VE (sin x) D. Е. None of the above
1. Problem 6.1.8 A. 2. sin x В. sin x С. V3(sin x) VE (sin x) D. Е. None of the above
Trigonometry (11th Edition)
11th Edition
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Chapter1: Trigonometric Functions
Section: Chapter Questions
Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Related questions
Question
simplify the expression
please answer this WITHOUT A CALCULATOR. THERE IS ONLY ONE ANSWER. answer choices are on first image.

Transcribed Image Text:1. Problem 6.1.8
A. \(2 \sin x\)
B. \(\sin x\)
C. \(\sqrt{3} (\sin x)\)
D. \(\sqrt{2} (\sin x)\)
E. None of the above
![**Problem 8:**
\[ \sin\left(x + \frac{\pi}{6}\right) + \sin\left(x - \frac{\pi}{6}\right) \]
This expression demonstrates the application of trigonometric identities involving sums and differences of angles. The sine addition and subtraction identities can be employed to simplify or evaluate the expression further:
\[ \sin(a \pm b) = \sin a \cos b \pm \cos a \sin b \]
Using these identities, one can break down the expression into known trigonometric values for further calculation or demonstration. Also, it illustrates how angle shifting impacts the sine of an angle.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fa3348a9c-7c7d-4999-b36a-cd8f5af69dd1%2F0d2be843-22c5-408e-b1e1-51e39fbdf6ab%2Ffcj6do_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem 8:**
\[ \sin\left(x + \frac{\pi}{6}\right) + \sin\left(x - \frac{\pi}{6}\right) \]
This expression demonstrates the application of trigonometric identities involving sums and differences of angles. The sine addition and subtraction identities can be employed to simplify or evaluate the expression further:
\[ \sin(a \pm b) = \sin a \cos b \pm \cos a \sin b \]
Using these identities, one can break down the expression into known trigonometric values for further calculation or demonstration. Also, it illustrates how angle shifting impacts the sine of an angle.
Expert Solution
Step 1
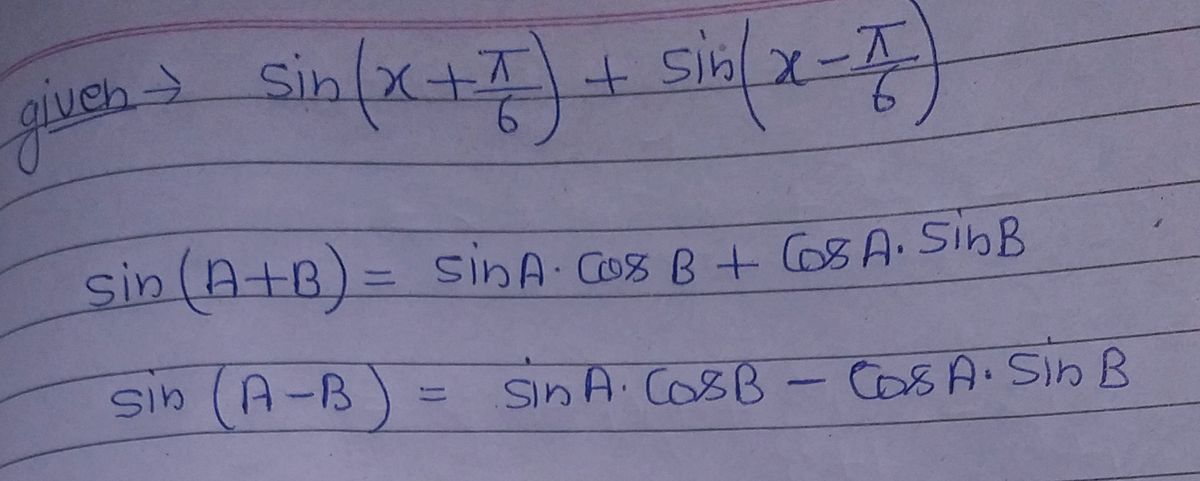
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning