1. For each of the following test z- test versus the t-test versus the chi squared test. Describe what the test is for and what conditions must be satisfied before test is conducted
1. For each of the following test z- test versus the t-test versus the chi squared test. Describe what the test is for and what conditions must be satisfied before test is conducted
2. give at least one example of two variables that have
t-test:
t-test for one sample: It is used to determine if there is any difference between the sample mean from some hypothesized mean.
The test statistic is given below:

The distribution of the test statistic follows student’s t-distribution with (n-1) degrees of freedom. The plot of t-distribution is same as of standard normal distribution, with only difference i.e., t-distribution’s probability curve has more spread and less peak.
Two sample t test is a statistical test applied to two samples which are dependent and paired observations are taken.
Conditions for a t-test:
- The sample size is small, n less than 30 but should not be less than 5.
- Standard deviation is not known
- Scale of measurement applied to the data collected follows a continuous or ordinal scale
- When a normal distribution is assumed, level of significance or p as a criterion for acceptance is specified.
- Standard deviations or samples are approximately equal.
Z-test:
It is a hypothesis test which is used to determine if there is a significant difference between means of two populations or to test the hypothesis about the mean of a population based on a single sample (or) to test the hypothesis about the proportion of successes in a single sample (or) the difference between the proportion of successes in two samples. This test is generally used for large samples drawn from a normal population.
It determines to what extent a data point is away from its mean of the data set, in standard deviation. The test statistic is given by:
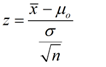

Condition for z-test:
- Sample size is large i.e., n>30
- Sampling distribution must be normal or approximately normal
- Population standard deviation is known.
Step by step
Solved in 4 steps with 5 images









