1. Each of the following limit expressions correspond to a limit definition of the derivative of a particular function at a specific point. Determine the function and the point for each expression. 3 cos(20) a. lim 0→π/4 0-7 b. lim h→0 ((1 + h)³ + 2(1 + h)² − 9) + 6 h
1. Each of the following limit expressions correspond to a limit definition of the derivative of a particular function at a specific point. Determine the function and the point for each expression. 3 cos(20) a. lim 0→π/4 0-7 b. lim h→0 ((1 + h)³ + 2(1 + h)² − 9) + 6 h
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
Hi, I need help with this one, I would really appreciate it if you could write it where I could read it. Thank you for your help! Please only use the formulas provided.

Transcribed Image Text:1. Each of the following limit expressions correspond to a limit definition of the derivative of a particular function at a
specific point. Determine the function and the point for each expression.
a.
lim
0→π/4
3 cos(20)
0-2
b.
lim
h→0
((1 + h)³ + 2(1 + h)² − 9) + 6
h
![MULTIPLE DERIVATIVES
A function fis-times differentiable (or fE C") if you can apply
the derivative times to fand have a continuous function after
each application of the derivative.
A function fis smooth (orf E C) if it can be differentiated
infinitely many times, and each derivative is a continuous
function
Linearity:
Products:
Quotients:
Compositions:
DERIVATIVE PROPERTIES
d
[f(x) + a· g(x)] = f(x) + a · g(x)
dx
d
dx
[ƒ(x)g (x)] = f(x)g (x) + f(x)g'(x)
d f(x)
dx [g(x)]
d
dx
f(x)g(x) = f(x)g'(x)
(g(x)) ²
where g(x) = 0
[ƒ (g(x))] = f(g(x)) · g'(x)
TANGENT AND NORMAL LINES
If y=f(x) describes some differentiable function, the equation of
the tangent line at a point
is given by
y = f(x)(x − a) + f(a).
The equation of the normal line at a point
(x-a) + f(a).
If fis differentiable near
f (a)
is given by
LINEAR APPROXIMATION
then for values close to,
f(x) = f(a)(x-a) + f(a).
Constant:
Power:
Exponential:
Logarithmic:
BASIC FUNCTION DERIVATIVES
Trigonometric:
Hyperbolic:
d
dx
d
dx
d
dx
d
dx
d
dx
d
d
[b] = ln(b) b*, where b € (0,0)
dx
d
dx
[a] = 0, where a
d
dx
M
dx
d
dx
d
dx
Inverse Trigonometric:
d
dx
d
dx
d
dx
=x²-¹, where
[log(x)] =
[sin(x)] = cos(x)
[cos(x)]=sin(x)
[tan(x)] = sec²(x)
[sec(x)] = sec(x)tan(x)
[cot(x)]=-csc²(x)
[csc(x)]=csc(x)cot(x)
[arcsin(x)]
[arccos(x)]
In(b) x
[arctan(x)]
1+x²
where b, x € (0,00)
[sinh(x)] = cosh(x)
[cosh(x)] = sinh(x)
where x = ±
where x ±
C
ZOOM +](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ff4b0f97a-89e5-4466-a6e2-73ccf61a13a9%2Ff699826f-4fbe-4a04-970a-2d35da7ba0ca%2Fg5e44dv_processed.png&w=3840&q=75)
Transcribed Image Text:MULTIPLE DERIVATIVES
A function fis-times differentiable (or fE C") if you can apply
the derivative times to fand have a continuous function after
each application of the derivative.
A function fis smooth (orf E C) if it can be differentiated
infinitely many times, and each derivative is a continuous
function
Linearity:
Products:
Quotients:
Compositions:
DERIVATIVE PROPERTIES
d
[f(x) + a· g(x)] = f(x) + a · g(x)
dx
d
dx
[ƒ(x)g (x)] = f(x)g (x) + f(x)g'(x)
d f(x)
dx [g(x)]
d
dx
f(x)g(x) = f(x)g'(x)
(g(x)) ²
where g(x) = 0
[ƒ (g(x))] = f(g(x)) · g'(x)
TANGENT AND NORMAL LINES
If y=f(x) describes some differentiable function, the equation of
the tangent line at a point
is given by
y = f(x)(x − a) + f(a).
The equation of the normal line at a point
(x-a) + f(a).
If fis differentiable near
f (a)
is given by
LINEAR APPROXIMATION
then for values close to,
f(x) = f(a)(x-a) + f(a).
Constant:
Power:
Exponential:
Logarithmic:
BASIC FUNCTION DERIVATIVES
Trigonometric:
Hyperbolic:
d
dx
d
dx
d
dx
d
dx
d
dx
d
d
[b] = ln(b) b*, where b € (0,0)
dx
d
dx
[a] = 0, where a
d
dx
M
dx
d
dx
d
dx
Inverse Trigonometric:
d
dx
d
dx
d
dx
=x²-¹, where
[log(x)] =
[sin(x)] = cos(x)
[cos(x)]=sin(x)
[tan(x)] = sec²(x)
[sec(x)] = sec(x)tan(x)
[cot(x)]=-csc²(x)
[csc(x)]=csc(x)cot(x)
[arcsin(x)]
[arccos(x)]
In(b) x
[arctan(x)]
1+x²
where b, x € (0,00)
[sinh(x)] = cosh(x)
[cosh(x)] = sinh(x)
where x = ±
where x ±
C
ZOOM +
Expert Solution
Step
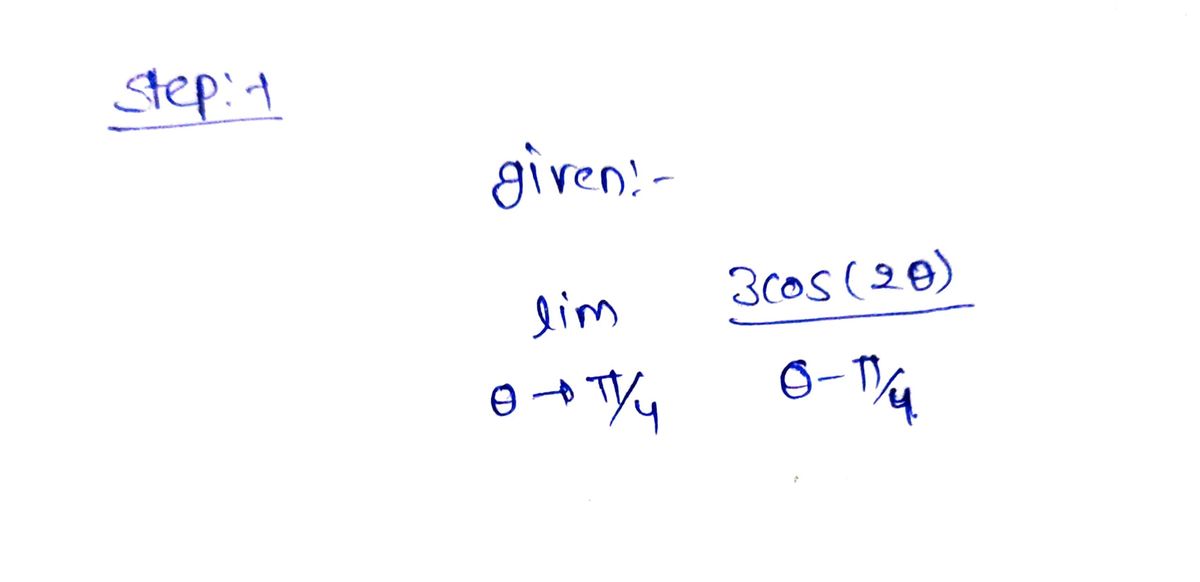
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning