(1 point) Complete the truth table for the following statement: P 9 TT TF FT FF ~p ~q (p^~g) ^ (~p V q) PA~q ~pvq (p^~q) ^ (~p V g)
(1 point) Complete the truth table for the following statement: P 9 TT TF FT FF ~p ~q (p^~g) ^ (~p V q) PA~q ~pvq (p^~q) ^ (~p V g)
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Truth Table Exercise**
**Objective**: Complete the truth table for the given logical statement:
\[ (p \land \neg q) \land (\neg p \lor q) \]
**Truth Table Layout**
The table consists of the following columns:
- **\( p \)** and **\( q \)**: These are the initial propositions, each of which can be True (T) or False (F).
- **\( \neg p \)**: The negation of \( p \).
- **\( \neg q \)**: The negation of \( q \).
- **\( p \land \neg q \)**: The conjunction (AND operation) of \( p \) and \( \neg q \).
- **\( \neg p \lor q \)**: The disjunction (OR operation) of \( \neg p \) and \( q \).
- **\[ (p \land \neg q) \land (\neg p \lor q) \]**: The full expression combining both parts as specified in the problem statement.
**Table Structure**:
| **p** | **q** | **\( \neg p \)** | **\( \neg q \)** | **\( p \land \neg q \)** | **\( \neg p \lor q \)** | **\[ (p \land \neg q) \land (\neg p \lor q) \]** |
|-------|-------|----------------|----------------|--------------------|------------------|------------------------------------------|
| T | T | | | | | |
| T | F | | | | | |
| F | T | | | | | |
| F | F | | | | | |
**Instructions**: Fill in each blank space based on the logical operations and given values of \( p \) and \( q \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F23af0884-495a-461c-9f7c-d263d97dbf10%2F74ed826f-8b4d-4d36-b1fa-32092baaab10%2F19eqotc_processed.png&w=3840&q=75)
Transcribed Image Text:**Truth Table Exercise**
**Objective**: Complete the truth table for the given logical statement:
\[ (p \land \neg q) \land (\neg p \lor q) \]
**Truth Table Layout**
The table consists of the following columns:
- **\( p \)** and **\( q \)**: These are the initial propositions, each of which can be True (T) or False (F).
- **\( \neg p \)**: The negation of \( p \).
- **\( \neg q \)**: The negation of \( q \).
- **\( p \land \neg q \)**: The conjunction (AND operation) of \( p \) and \( \neg q \).
- **\( \neg p \lor q \)**: The disjunction (OR operation) of \( \neg p \) and \( q \).
- **\[ (p \land \neg q) \land (\neg p \lor q) \]**: The full expression combining both parts as specified in the problem statement.
**Table Structure**:
| **p** | **q** | **\( \neg p \)** | **\( \neg q \)** | **\( p \land \neg q \)** | **\( \neg p \lor q \)** | **\[ (p \land \neg q) \land (\neg p \lor q) \]** |
|-------|-------|----------------|----------------|--------------------|------------------|------------------------------------------|
| T | T | | | | | |
| T | F | | | | | |
| F | T | | | | | |
| F | F | | | | | |
**Instructions**: Fill in each blank space based on the logical operations and given values of \( p \) and \( q \).
Expert Solution
Step 1
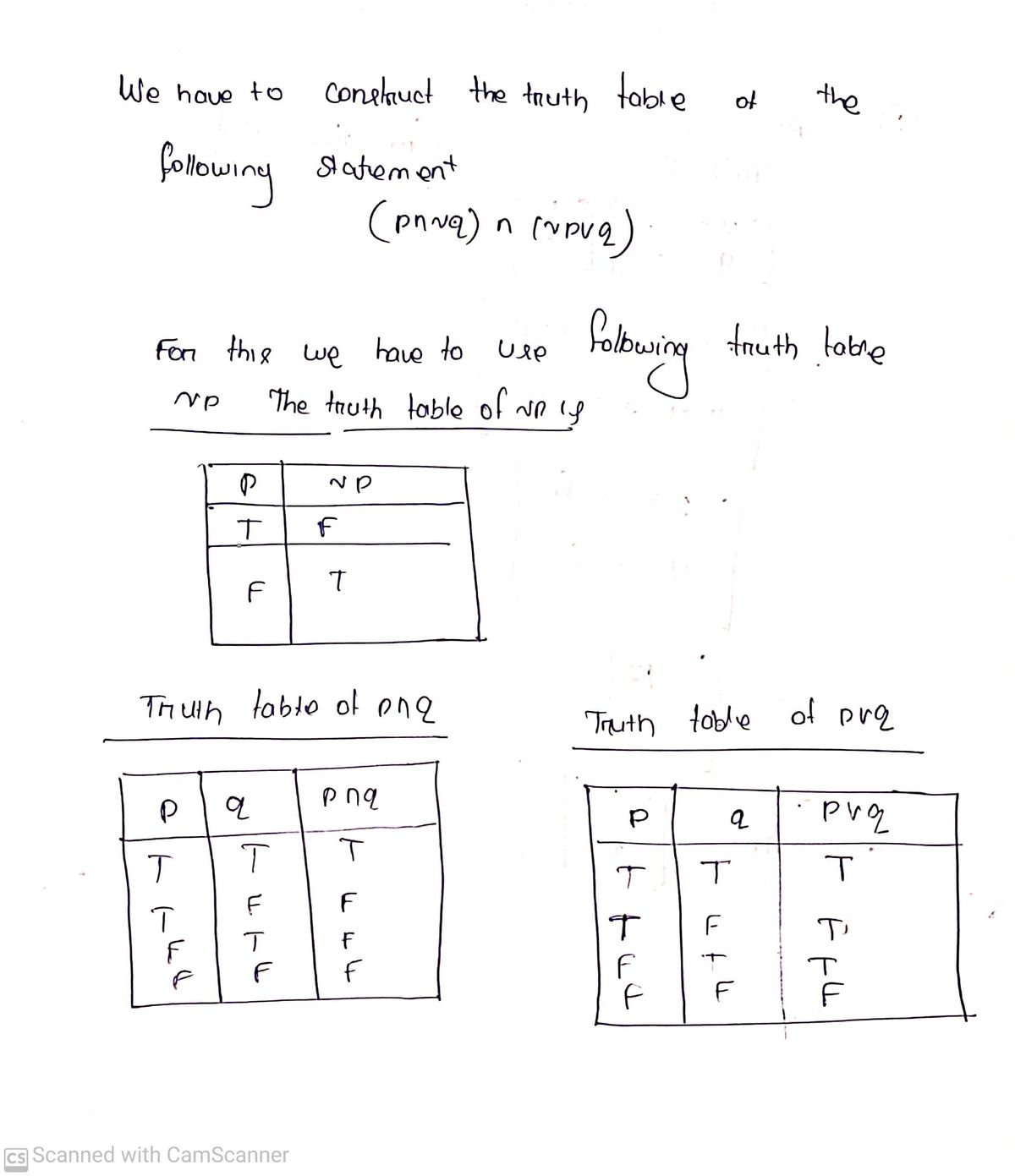
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

