Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
![**Problem Statement:**
Let \( h(u) = 4u^3 - \frac{1}{u^2} \).
**Task:**
Find \( h'(u) \). Show your work.
---
**Solution:**
To find \( h'(u) \), we will differentiate each term of the function \( h(u) \) separately using the rules of differentiation.
1. Differentiate the first term \( 4u^3 \).
- The derivative of \( u^n \) is \( nu^{n-1} \).
- Therefore, the derivative of \( 4u^3 \) is:
\[
4 \times 3u^{3-1} = 12u^2
\]
2. Differentiate the second term \( -\frac{1}{u^2} \).
- Rewrite \( \frac{1}{u^2} \) as \( u^{-2} \).
- The derivative of \( u^{-n} \) is \( -nu^{-n-1} \).
- Therefore, the derivative of \( u^{-2} \) is:
\[
-(-2)u^{-2-1} = 2u^{-3}
\]
- This simplifies to \( \frac{2}{u^3} \).
**Final Derivative:**
Combine the results to find \( h'(u) \):
\[
h'(u) = 12u^2 + \frac{2}{u^3}
\]
Thus, the derivative of \( h(u) \) is \( h'(u) = 12u^2 + \frac{2}{u^3} \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fd556e803-222c-475e-bc6a-44d8250d1cd2%2F7169f523-08bb-45c0-a020-aff1cb32076c%2Fm5n6ixt_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Let \( h(u) = 4u^3 - \frac{1}{u^2} \).
**Task:**
Find \( h'(u) \). Show your work.
---
**Solution:**
To find \( h'(u) \), we will differentiate each term of the function \( h(u) \) separately using the rules of differentiation.
1. Differentiate the first term \( 4u^3 \).
- The derivative of \( u^n \) is \( nu^{n-1} \).
- Therefore, the derivative of \( 4u^3 \) is:
\[
4 \times 3u^{3-1} = 12u^2
\]
2. Differentiate the second term \( -\frac{1}{u^2} \).
- Rewrite \( \frac{1}{u^2} \) as \( u^{-2} \).
- The derivative of \( u^{-n} \) is \( -nu^{-n-1} \).
- Therefore, the derivative of \( u^{-2} \) is:
\[
-(-2)u^{-2-1} = 2u^{-3}
\]
- This simplifies to \( \frac{2}{u^3} \).
**Final Derivative:**
Combine the results to find \( h'(u) \):
\[
h'(u) = 12u^2 + \frac{2}{u^3}
\]
Thus, the derivative of \( h(u) \) is \( h'(u) = 12u^2 + \frac{2}{u^3} \).
Expert Solution
Step 1
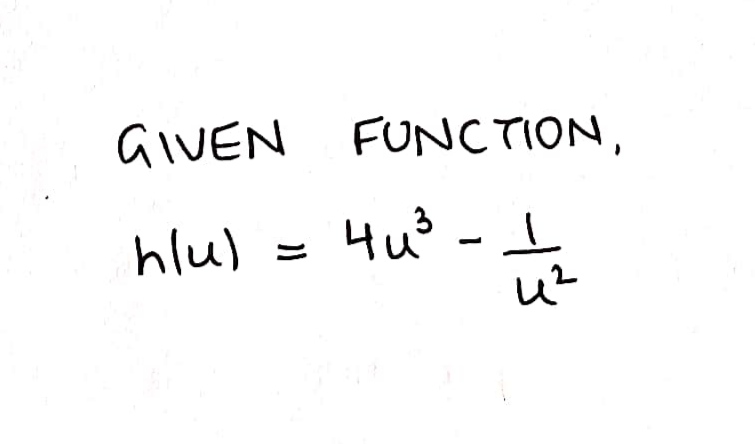
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning