[(@1 + a3 + a5) - (a2 + a4)] [(B1 + B3 + B3) + A (B2 + B4)]' P+Q = (4.17) %3D while, by adding (4.15) and (4.16) and by using the relation p² + Q? = (P+Q)² – 2PQ for al P,Q E R, we have [(a1 + a3 + a5) - (a2 + a4)] [(B1 + B3 + B5) (a2 + a4) + A (B2 + B4) (a1 + a3 + a5)] PQ [(B1 + B3 + B3) + A (B2 + B4)]² [((B2 + B4) – (B1 + B3 + B5)) (A+1)] (4.18) Let P and Q are two distinct real roots of the quadratic equation
[(@1 + a3 + a5) - (a2 + a4)] [(B1 + B3 + B3) + A (B2 + B4)]' P+Q = (4.17) %3D while, by adding (4.15) and (4.16) and by using the relation p² + Q? = (P+Q)² – 2PQ for al P,Q E R, we have [(a1 + a3 + a5) - (a2 + a4)] [(B1 + B3 + B5) (a2 + a4) + A (B2 + B4) (a1 + a3 + a5)] PQ [(B1 + B3 + B3) + A (B2 + B4)]² [((B2 + B4) – (B1 + B3 + B5)) (A+1)] (4.18) Let P and Q are two distinct real roots of the quadratic equation
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Topic Video
Question
Show me the steps of determine yellow and the informatian is here
![The main focus of this article is to discuss some qualitative behavior of
the solutions of the nonlinear difference equation
a1Ym-1+a2Ym-2+ a3Ym-3+ a4Ym–4+ a5Ym-5
Ут+1 — Аутt
т 3 0, 1, 2, ...,
B1Ym-1+ B2Ym-2 + B3Ym-3 + B4Ym-4 + B3Ym-5
(1.1)
where the coefficients A, a;, B; E (0, 0), i = 1, ..., 5, while the initial condi-
tions y-5,y-4,Y–3,Y–2, Y–1, yo are arbitrary positive real numbers. Note that
the special case of Eq.(1.1) has been discussed in [4] when az = B3 = a4 =
= a5 = B5 = 0 and Eq.(1.1) has been studied in [8] in the special case
B4
when a4 =
B4 = a5 = B5 = 0 and Eq.(1.1) has been discussed in [5] in the
special case when az = B5 = 0.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F7ecaae78-467a-4f8b-9627-a81f9986c070%2Fcc6ab89c-5e28-4dec-a0ef-bf65b2ee82a8%2Fdtsy4hk_processed.jpeg&w=3840&q=75)
Transcribed Image Text:The main focus of this article is to discuss some qualitative behavior of
the solutions of the nonlinear difference equation
a1Ym-1+a2Ym-2+ a3Ym-3+ a4Ym–4+ a5Ym-5
Ут+1 — Аутt
т 3 0, 1, 2, ...,
B1Ym-1+ B2Ym-2 + B3Ym-3 + B4Ym-4 + B3Ym-5
(1.1)
where the coefficients A, a;, B; E (0, 0), i = 1, ..., 5, while the initial condi-
tions y-5,y-4,Y–3,Y–2, Y–1, yo are arbitrary positive real numbers. Note that
the special case of Eq.(1.1) has been discussed in [4] when az = B3 = a4 =
= a5 = B5 = 0 and Eq.(1.1) has been studied in [8] in the special case
B4
when a4 =
B4 = a5 = B5 = 0 and Eq.(1.1) has been discussed in [5] in the
special case when az = B5 = 0.
![Theorem 6 If (a1 + a3 + a5) > (a2 + a4) and (B1 + B3 + B5) > (B2 + B4),
then the necessary and sufficient condition for Eq.(1.1) to have positive so-
lutions of prime period two is that the inequality
[(A+ 1) ((B1 + B3 + Bs) – (B2 + B4)] [(a1 + a3 + as) – (a2 + a4)]?
+4 [(a1 + a3 + a5) – (a2 + a4)] [(B1 + B3 + Bs) (a2 + a4) + A (B2 + B4) (a1 + az + as)] > 0.
(4.13)
is valid.
proof: Suppose there exist positive distinctive solutions of prime period
two
..., P, Q, P,Q, .....
of Eq.(1.1). From Eq.(1.1) we have
a1Ym–1+a2Ym–2+a3Ym-3+¤4Ym-4+a5Ym–5
Ym+1 = Aym+
Biym-1 + B2ym-2 + B3Ym-3 + B4Ym-4 + B5Ym-5
(a1 + a3 + a5)P+ (a2 + a4) Q
(B1 + B3 + Bs) P+(B2 + B4) Q
(a1 + a3 + a5) Q+ (a2 + a4) P
(B1 + B3 + Bs) Q+ (B2 + B4) P
(4.14)
P = AQ+
Q = AP+
Consequently, we get
(B1 + B3 + Bs) P² + (B2 + B4) PQ = A(B1+ B3 + B5) PQ + A (B2 + B4) Q?
+(a1+ a3 + a5) P+ (a2+a4) Q,
(4.15)
and
(B1 + B3 + B3) Q² + (B2 + B4) PQ = A (B1 + B3 + B5) PQ + A (B2 + B4) p²
+ (a1 + a3 + a5) Q+ (a2 + a4) P.
(4.16)
By subtracting (4.15) from (4.16), we obtain
[(B1 + B3 + Bs) + A (B2 + B4)] (P² – Q²) = [(a1 + a3 +a5) – (a2 + a4)] (P – Q).
11
Since P+ Q, it follows that
[(a1 + a3 + a5) – (a2 + a4)]
[(B1 + B3 + B5) + A (B2 + B4)]'
P+Q =
(4.17)
while, by adding (4.15) and (4.16) and by using the relation
p² + Q? = (P+ Q)² – 2PQ for all
P,Q ER,
we have
[(a1 + az + a5) - (a2 + a4)] [(B1 + B3 + Bs) (a2 + a4) + A (B2 + B4) (a1 + az + a5)]
[(B1 + B3 + B5) + A (B2 + B4)]* [((B2 + B4) – (B1 + B3 + B5)) (A+1)]
PQ =
(4.18)
Let P and Q are two distinct real roots of the quadratic equation
t2 - (P+ Q)t + PQ = 0.
[(B1 + B3 + B5) + A (B2 + B4)] t – [(@1 + a3 + a5) – (a2 + a4)]t
[(a1 + az + a5) - (a2 + a4)] [(B1 + B3 + B5) (a2 + a4) + A (B2 + B4) (a1 + a3 + a5)]
+
[(81 + B3 + B5) + A (B2 + B4)] [((B2 + B4) – (B1 + B3 + Bs)) (A+1)]
0,
(4.19)](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F7ecaae78-467a-4f8b-9627-a81f9986c070%2Fcc6ab89c-5e28-4dec-a0ef-bf65b2ee82a8%2Fj6rmyvn_processed.png&w=3840&q=75)
Transcribed Image Text:Theorem 6 If (a1 + a3 + a5) > (a2 + a4) and (B1 + B3 + B5) > (B2 + B4),
then the necessary and sufficient condition for Eq.(1.1) to have positive so-
lutions of prime period two is that the inequality
[(A+ 1) ((B1 + B3 + Bs) – (B2 + B4)] [(a1 + a3 + as) – (a2 + a4)]?
+4 [(a1 + a3 + a5) – (a2 + a4)] [(B1 + B3 + Bs) (a2 + a4) + A (B2 + B4) (a1 + az + as)] > 0.
(4.13)
is valid.
proof: Suppose there exist positive distinctive solutions of prime period
two
..., P, Q, P,Q, .....
of Eq.(1.1). From Eq.(1.1) we have
a1Ym–1+a2Ym–2+a3Ym-3+¤4Ym-4+a5Ym–5
Ym+1 = Aym+
Biym-1 + B2ym-2 + B3Ym-3 + B4Ym-4 + B5Ym-5
(a1 + a3 + a5)P+ (a2 + a4) Q
(B1 + B3 + Bs) P+(B2 + B4) Q
(a1 + a3 + a5) Q+ (a2 + a4) P
(B1 + B3 + Bs) Q+ (B2 + B4) P
(4.14)
P = AQ+
Q = AP+
Consequently, we get
(B1 + B3 + Bs) P² + (B2 + B4) PQ = A(B1+ B3 + B5) PQ + A (B2 + B4) Q?
+(a1+ a3 + a5) P+ (a2+a4) Q,
(4.15)
and
(B1 + B3 + B3) Q² + (B2 + B4) PQ = A (B1 + B3 + B5) PQ + A (B2 + B4) p²
+ (a1 + a3 + a5) Q+ (a2 + a4) P.
(4.16)
By subtracting (4.15) from (4.16), we obtain
[(B1 + B3 + Bs) + A (B2 + B4)] (P² – Q²) = [(a1 + a3 +a5) – (a2 + a4)] (P – Q).
11
Since P+ Q, it follows that
[(a1 + a3 + a5) – (a2 + a4)]
[(B1 + B3 + B5) + A (B2 + B4)]'
P+Q =
(4.17)
while, by adding (4.15) and (4.16) and by using the relation
p² + Q? = (P+ Q)² – 2PQ for all
P,Q ER,
we have
[(a1 + az + a5) - (a2 + a4)] [(B1 + B3 + Bs) (a2 + a4) + A (B2 + B4) (a1 + az + a5)]
[(B1 + B3 + B5) + A (B2 + B4)]* [((B2 + B4) – (B1 + B3 + B5)) (A+1)]
PQ =
(4.18)
Let P and Q are two distinct real roots of the quadratic equation
t2 - (P+ Q)t + PQ = 0.
[(B1 + B3 + B5) + A (B2 + B4)] t – [(@1 + a3 + a5) – (a2 + a4)]t
[(a1 + az + a5) - (a2 + a4)] [(B1 + B3 + B5) (a2 + a4) + A (B2 + B4) (a1 + a3 + a5)]
+
[(81 + B3 + B5) + A (B2 + B4)] [((B2 + B4) – (B1 + B3 + Bs)) (A+1)]
0,
(4.19)
Expert Solution
Step 1
Given:
It is given that, the value of P and Q is as follows:
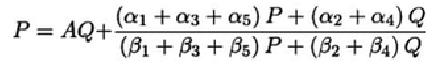...... (1)
and
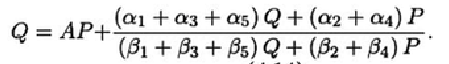......(2)
To prove:
we have to prove that,
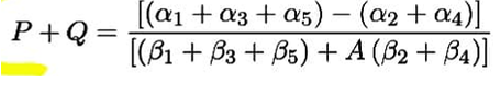
and
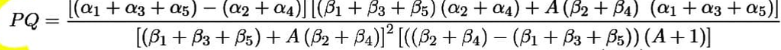
Step by step
Solved in 3 steps with 4 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
