1 {a,}={ 4. Let | 2n² Let ɛ =.001. Find a natural number N such that |a, - L<ɛ when n 2 N.
1 {a,}={ 4. Let | 2n² Let ɛ =.001. Find a natural number N such that |a, - L<ɛ when n 2 N.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Concept explainers
Ratios
A ratio is a comparison between two numbers of the same kind. It represents how many times one number contains another. It also represents how small or large one number is compared to the other.
Trigonometric Ratios
Trigonometric ratios give values of trigonometric functions. It always deals with triangles that have one angle measuring 90 degrees. These triangles are right-angled. We take the ratio of sides of these triangles.
Question
need assitance if possible

Transcribed Image Text:**Problem Statement:**
4. Let \( \{ a_n \} = \left\{ \frac{1}{2n^2} \right\} \).
Let \( \varepsilon = 0.001 \).
Find a natural number \( N \) such that \( | a_n - L | < \varepsilon \) when \( n \geq N \).
**Explanation:**
This problem deals with sequences and limits. The sequence is defined as \( \{ a_n \} = \left\{ \frac{1}{2n^2} \right\} \). The task is to find a natural number \( N \) such that for all \( n \) greater than or equal to \( N \), the absolute difference between the sequence term \( a_n \) and the limit \( L \) is less than the small positive number \( \varepsilon = 0.001 \).
The underlying concept is the definition of convergence in sequences, where \( L \) is the limit that the sequence approaches as \( n \) becomes very large. In this case, the limit \( L \) is 0, because as \( n \) approaches infinity, \( \frac{1}{2n^2} \) approaches 0. Therefore, the goal is to identify \( N \) such that for every \( n \geq N \), the inequality \( \left| \frac{1}{2n^2} - 0 \right| < 0.001 \) holds.
Expert Solution
Step 1:Limit.
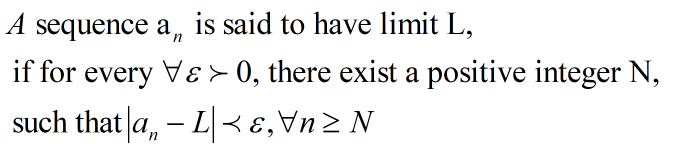
Step by step
Solved in 2 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

