Answered: A process considered to be in control…

Practical Management Science

6th Edition

ISBN:9781337406659

Author:WINSTON, Wayne L.

Publisher:WINSTON, Wayne L.

Chapter2: Introduction To Spreadsheet Modeling

Section: Chapter Questions

Problem 20P: Julie James is opening a lemonade stand. She believes the fixed cost per week of running the stand...

See similar textbooks

Related questions

Question

100%

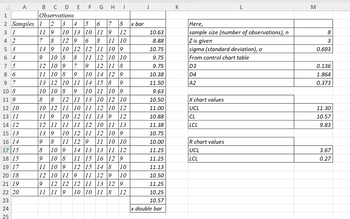
A process considered to be in control measures an ingredient in ounces.

Roberto Baggio, a quality inspector took 20 samples, each with 8 observations as follows:

thats in the pictuer

after that using this information, obtain three-sigma (i.e., z=3) control limits for a mean control chart and control limits for a range chart, respectively. It is known from previous experience that the standard deviation of the process is 0.693.

First: perform all actions and calculations needed to answer the question.

All equations/calculations needed to be fully written STEP by STEP. No short calculations or direct answers/results will be accepted.

This applies to the calculations for both types of control limits (mean and range).

Second: Explain the process followed to identify each type of control limit and any observations made in the problem-solving process.

thank you very much

SAMPLES
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
15
17
18
19
20
1
11
7
13
9
12
11
13
10
8
10
11
12
13
9
8
9
11
12
9
11
2
9
8
o
9
10
10
10
12
10
8
12
9
11
9
8
10
10
10
10
12
11
OBSERVATIONS
3
10
12
10
8
9
8
10
8
12
11
10
11
10
11
9
8
9
11
12
9
4
13
9
∞56
12
8
7
9
11
9
11
10
12
11
12
12
14
11
12
9
12
10
5
10
6
12
11
9
10
14
10
13
11
11
12
11
9
13
15
15
11
11
10
LO
6
11
8
11
12
12
14
15
11
10
12
13
10
12
11
13
16
14
12
13
11
11
7
9
11
10
10
11
12
8
10
12
10
9
10
10
11
12
8
9
12
8
8
12
10
9
10
8
aa
9
9
9
10
12
12
13
9
10
12
Ñ
9
10
10
9
12

Expert Solution

Trending now

This is a popular solution!

Step by step

Solved in 5 steps with 10 images

SEE SOLUTION Check out a sample Q&A here

Follow-up Questions

Read through expert solutions to related follow-up questions below.

Follow-up Question

thank you for your answer i found something similar on bertleby but the working out is different and the answers are slighilty different too i am not sure which one to use:

this is the answer that i found:

this are his answers but in the picture is working out

X chart values

UCL 11.30

CL 10.57

LCL 9.83

R chart values

UCL 3.67

LCL 0.27