1 16. Let the adjacency matrix for a relation R on the set {a, b, c) be given by 0 1 1 0 is the composition of R with itself, which ordered pair belongs to R²? O (b,c) O (c,b) O (b,a) 1 none of these 0 0. If R² 0
1 16. Let the adjacency matrix for a relation R on the set {a, b, c) be given by 0 1 1 0 is the composition of R with itself, which ordered pair belongs to R²? O (b,c) O (c,b) O (b,a) 1 none of these 0 0. If R² 0
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Matrix Relations and Composition**
**Problem 16:**
Consider the adjacency matrix for a relation \( R \) on the set \(\{a, b, c\}\), given by:
\[
\begin{bmatrix}
1 & 1 & 0 \\
0 & 1 & 0 \\
1 & 0 & 0
\end{bmatrix}
\]
If \( R^2 \) is the composition of \( R \) with itself, which ordered pair belongs to \( R^2 \)?
- (b, c)
- (c, b)
- (b, a)
- none of these
**Explanation:**
An adjacency matrix represents a relation on a set, where each element of the matrix indicates whether a pair of elements in the set is related. The entry at the \(i\)-th row and \(j\)-th column is \(1\) if the element corresponding to the \(i\)-th row is related to the element corresponding to the \(j\)-th column, and \(0\) otherwise.
The composition \( R^2 \) involves matrix multiplication of \( R \) with itself. By performing this operation, we can determine which new pairs in the set are related under the composition. The goal is to identify the correct ordered pair from the options provided that appears in \( R^2 \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F9348d578-66ea-4064-b97e-301aeae52239%2Ffa0921af-314b-481c-b483-dbfc2d9a39a4%2Fa2x2wu_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Matrix Relations and Composition**
**Problem 16:**
Consider the adjacency matrix for a relation \( R \) on the set \(\{a, b, c\}\), given by:
\[
\begin{bmatrix}
1 & 1 & 0 \\
0 & 1 & 0 \\
1 & 0 & 0
\end{bmatrix}
\]
If \( R^2 \) is the composition of \( R \) with itself, which ordered pair belongs to \( R^2 \)?
- (b, c)
- (c, b)
- (b, a)
- none of these
**Explanation:**
An adjacency matrix represents a relation on a set, where each element of the matrix indicates whether a pair of elements in the set is related. The entry at the \(i\)-th row and \(j\)-th column is \(1\) if the element corresponding to the \(i\)-th row is related to the element corresponding to the \(j\)-th column, and \(0\) otherwise.
The composition \( R^2 \) involves matrix multiplication of \( R \) with itself. By performing this operation, we can determine which new pairs in the set are related under the composition. The goal is to identify the correct ordered pair from the options provided that appears in \( R^2 \).
Expert Solution
Step 1
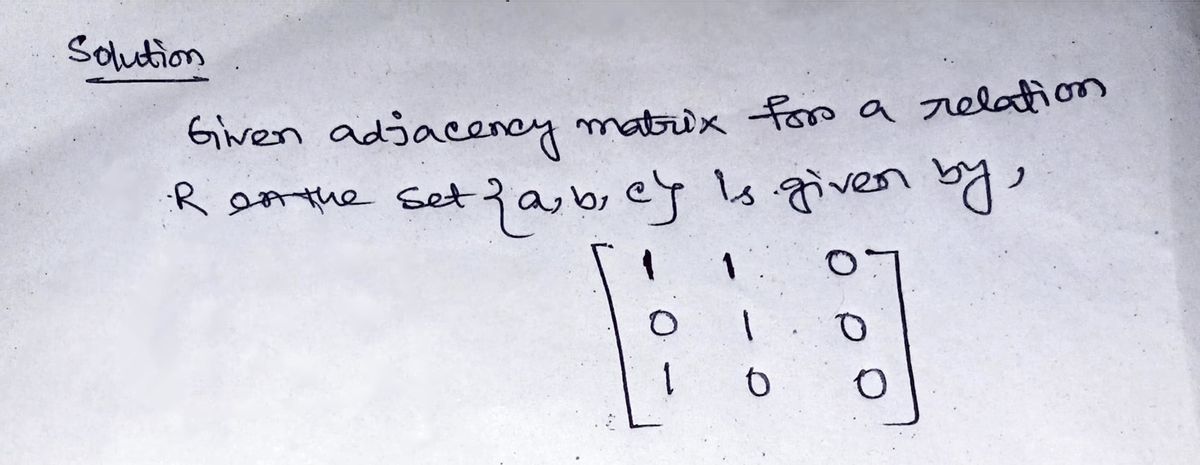
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

