. Solve the system given below using the method of your choice. X1 – 2x2 + x3 = 5 Xi + x2 – x3 = 0 X2 – x3 = 1
. Solve the system given below using the method of your choice. X1 – 2x2 + x3 = 5 Xi + x2 – x3 = 0 X2 – x3 = 1
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Problem 5: Solving a System of Linear Equations**
Solve the system given below using the method of your choice:
\[
x_1 - 2x_2 + x_3 = 5
\]
\[
x_1 + x_2 - x_3 = 0
\]
\[
x_2 - x_3 = 1
\]
In this problem, you are required to determine the values of \(x_1\), \(x_2\), and \(x_3\) that satisfy all three linear equations simultaneously. You can use a variety of methods such as substitution, elimination, or matrix operations like the Gaussian elimination method to find a solution.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fdfe80350-6fa1-469d-aae2-95b4dd3aa499%2F645d5504-49ba-4ddb-9e57-db29857784f8%2Fn6r9pi_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem 5: Solving a System of Linear Equations**
Solve the system given below using the method of your choice:
\[
x_1 - 2x_2 + x_3 = 5
\]
\[
x_1 + x_2 - x_3 = 0
\]
\[
x_2 - x_3 = 1
\]
In this problem, you are required to determine the values of \(x_1\), \(x_2\), and \(x_3\) that satisfy all three linear equations simultaneously. You can use a variety of methods such as substitution, elimination, or matrix operations like the Gaussian elimination method to find a solution.
Expert Solution
Step 1
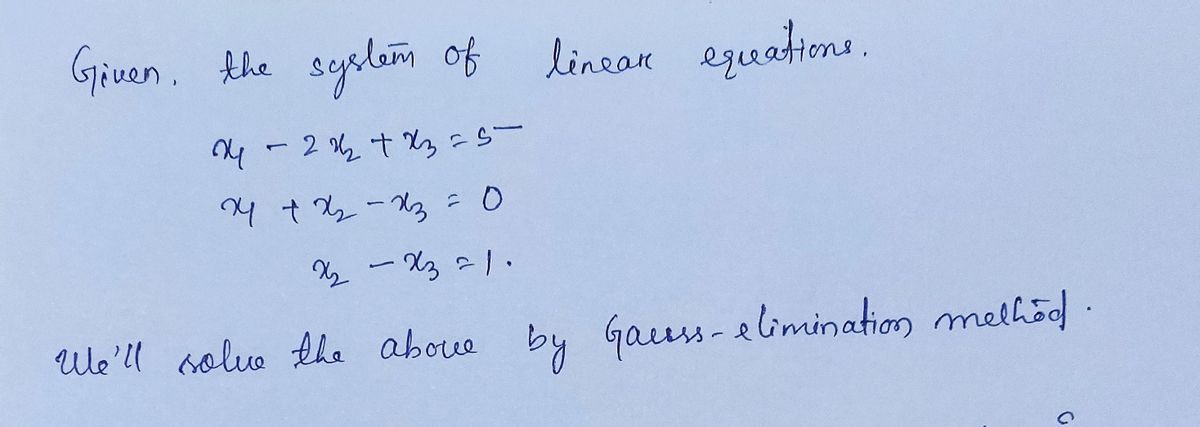
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

