. Either a mixed column or mixed row strategy is given. Use the given payoff matrix and find the optimal pure strategy (or strategies) the other player should use. Express the answer as a row or column matrix. Also determine the resulting expected payoff. ГО -1 5 P = 2-2 4 3 0 0 1 0-5
. Either a mixed column or mixed row strategy is given. Use the given payoff matrix and find the optimal pure strategy (or strategies) the other player should use. Express the answer as a row or column matrix. Also determine the resulting expected payoff. ГО -1 5 P = 2-2 4 3 0 0 1 0-5
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Either a mixed column or mixed row strategy is given. Use the given payoff matrix and find the optimal pure strategy (or strategies) the other player should use. Express the answer as a row or column matrix. Also determine the resulting expected payoff.
![The text appears to provide instructions related to game theory, specifically involving strategies and payoff matrices. Here's a breakdown suitable for an educational website:
---
**Game Theory Strategy Analysis**
In this exercise, we analyze either a mixed column or mixed row strategy using a given payoff matrix. The goal is to identify the optimal pure strategy (or strategies) the other player should use. The answer should be expressed as either a row or column matrix, and the resulting expected payoff should be determined.
**Payoff Matrix (P):**
\[
P = \begin{bmatrix}
0 & -1 & 5 \\
2 & -2 & 4 \\
0 & 3 & 0 \\
1 & 0 & -5
\end{bmatrix}
\]
**Task a:**
Given a mixed strategy column vector \( C \), defined as:
\[
C = \begin{bmatrix}
\frac{1}{3} \\
\frac{1}{3} \\
\frac{1}{3}
\end{bmatrix}^T
\]
Determine the optimal strategy for the row player and the expected payoff.
**Task b:**
Given a mixed strategy row vector \( R \), defined as:
\[
R = \begin{bmatrix}
0.8 & 0.2 & 0 & 0
\end{bmatrix}
\]
Determine the optimal strategy for the column player and the expected payoff.
---
For each part, students should calculate the expected payoffs by using the strategies provided and find the best response for the opposing player based on the payoff matrix. Students should apply concepts of mixed strategies and expected values to solve the problem.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F9a670ca7-8bea-4835-b14f-d42c1bdbe3d1%2Fe422cda9-697b-429d-9496-96e01371e8f0%2F4sx7etd_processed.png&w=3840&q=75)
Transcribed Image Text:The text appears to provide instructions related to game theory, specifically involving strategies and payoff matrices. Here's a breakdown suitable for an educational website:
---
**Game Theory Strategy Analysis**
In this exercise, we analyze either a mixed column or mixed row strategy using a given payoff matrix. The goal is to identify the optimal pure strategy (or strategies) the other player should use. The answer should be expressed as either a row or column matrix, and the resulting expected payoff should be determined.
**Payoff Matrix (P):**
\[
P = \begin{bmatrix}
0 & -1 & 5 \\
2 & -2 & 4 \\
0 & 3 & 0 \\
1 & 0 & -5
\end{bmatrix}
\]
**Task a:**
Given a mixed strategy column vector \( C \), defined as:
\[
C = \begin{bmatrix}
\frac{1}{3} \\
\frac{1}{3} \\
\frac{1}{3}
\end{bmatrix}^T
\]
Determine the optimal strategy for the row player and the expected payoff.
**Task b:**
Given a mixed strategy row vector \( R \), defined as:
\[
R = \begin{bmatrix}
0.8 & 0.2 & 0 & 0
\end{bmatrix}
\]
Determine the optimal strategy for the column player and the expected payoff.
---
For each part, students should calculate the expected payoffs by using the strategies provided and find the best response for the opposing player based on the payoff matrix. Students should apply concepts of mixed strategies and expected values to solve the problem.
Expert Solution
Step 1
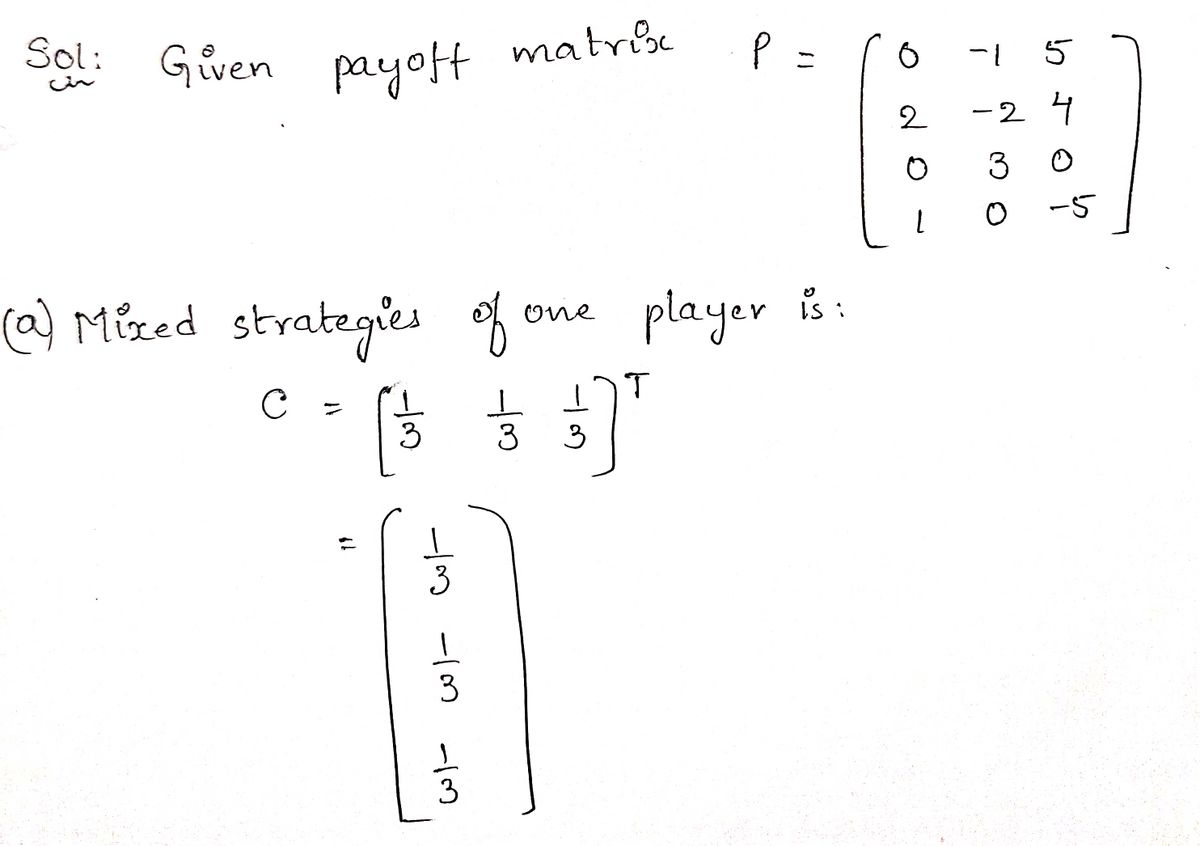
Step by step
Solved in 7 steps with 6 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

