
Concept explainers
Expand Your knowledge: Continuous Uniform
Let
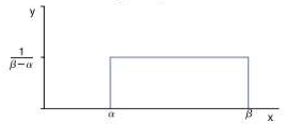
The base of the rectangle has length
must lie between
Now suppose that a and b are numbers such that

Because x is chosen at random from [a, b], the area of the rectangle that lies above [a, b] is the probability that x lies in
In this way. we can assign a probability to any interval inside |a. b|. This probability distribution is called the continuous uniform distribution (also called the rectangular distribution). Using some extra mathematics, it can be shown that if x is a random variable with this distribution, then the mean and standard deviation of x are
Sedimentation experiments are very important in the study of biology, medicine, hydrodynamics, petroleum engineering, civil engineering, and so on. The size (diameter) of approximately spherical particles is important since larger particles hinder and sometimes Mock the movement of smaller particles. Usually the size of sediment particles follows a uniform distribution (Reference: Y. Zimmels, "Theory of Kindred Sedimentation of Poly disperse Mixtures.” AIChE Journal, Vol. 29. No. 4. pp. 669-676).
Suppose a veterinary science experiment injects very small, spherical pellets of low-level radiation directly into an animal’s bloodstream The purpose is to attempt to cure a form of recurring cancer. The pellets eventually dissolve and pass through the animal's system. Diameters of the pellets are uniformly distributed from 0.015 mm to 0.065 mm If a pellet enters an artery, what is the probability that it will be the following sizes?
(a) 0.050 mm or larger. Hint: All particles are between 0.015 mm and 0.065 mm, so larger than 0.050 means
(b) 0.040 mm or smaller
(c) between 0.035 mm and 0.055 mm
(d) Compute the mean size of the particles.
(e) Compute the standard deviation of panicle size.
Trending nowThis is a popular solution!

Chapter 7 Solutions
Bundle: Understanding Basic Statistics, Loose-leaf Version, 7th + WebAssign Printed Access Card for Brase/Brase's Understanding Basic Statistics, ... for Peck's Statistics: Learning from Data
- Assume that the probability that an airplane engine will fail during a torture test is 12and that the aircraft in question has 4 engines. Construct a sample space for the torture test. Use S for survive and F for fail.arrow_forwardDetermine if the statement is true or false. If the statement is false, then correct it and make it true. The probability that an event occurs can be a negative number.arrow_forwardFind the probability of each event. Getting 2 red eggs in a single scoop from a bucket containing 5 red eggs and 7 yellow eggsarrow_forward
- If a binomial experiment has probability p success, then the probability of failure is ____________________. The probability of getting exactly r successes in n trials of this experiment is C(_________, _________)p (1p)arrow_forwardThe conditional probability of E given that F occurs is P(EF)=___________. So in rolling a die the conditional probability of the event E, getting a six, given that the event F, getting an even number, has occurred is P(EF)=___________.arrow_forwardAssume that the probability that an airplane engine will fail during a torture test is 12and that the aircraft in question has 4 engines. Find the probability that all engines will survive the test.arrow_forward
 College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning




