Chapter 6.9, Problem 1AE

Biology A strain of E-coli Beu 397-recA441 is placed into a nutrient broth at ${30}^{\circ }$ Celsius and allowed to grow. The following data are collected. Theory states that the number of bacteria in the petri dish will initially grow according to the law of uninhibited growth. The population is measured using an optical device in which the amount of light that passes through the petri dish is measured.

(a) Draw a scatter diagram treating time as the independent variable.

(b) Using a graphing utility, build an exponential model from the data.

(c) Express the function found in part (b) in the form $N(t)=N_0{e}^{kt}$.

(d) Graph the exponential function found in part (b) or (c) on the scatter diagram.

(e) Use the exponential function from part (b) or (c) to predict the population at $x=7$ hours.

(f) Use the exponential function from part (b) or (c) to predict when the population will reach $0.75$.

To determine

To answer: The questions based on the given data in the table.

Answer to Problem 1AE

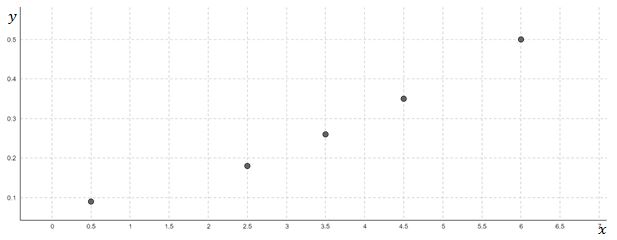
a. Scatter diagram.

Explanation of Solution

Given:

Table:

Time (hours), $x$	Population, $y$
0	$0.09$
$2.5$	$0.18$
$3.5$	$0.26$
$4.5$	$0.35$
6	$0.50$

Calculation:

a. Scatter diagram.

Enter the data into the graphical utility, the time in $x\text{-axis}$ and the population in $y\text{-axis}$, we obtain the scatter diagram as shown below.

To determine

To answer: The questions based on the given data in the table.

Answer to Problem 1AE

b. $y=0.090311284\cdot {\left(1.3384277\right)}^x$; $R^2=0.9927$

Explanation of Solution

Given:

Table:

Time (hours), $x$	Population, $y$
0	$0.09$
$2.5$	$0.18$
$3.5$	$0.26$
$4.5$	$0.35$
6	$0.50$

Calculation:

b.

The exponential function is of the form $y=a{b}^x$. Using the option of in the form $N\left(t\right)=N_o{e}^{kt}$, where $x=t$ and $y=N\left(t\right)$, proceed as follows:

$y=0.090311284\cdot {\left(1.3384277\right)}^x$; $R^2=0.9927$

To determine

To answer: The questions based on the given data in the table.

Answer to Problem 1AE

c. $N\left(t\right)=0.090311284e^{0.2915t}$

Explanation of Solution

Given:

Table:

Time (hours), $x$	Population, $y$
0	$0.09$
$2.5$	$0.18$
$3.5$	$0.26$
$4.5$	$0.35$
6	$0.50$

Calculation:

c.

To express $y=a{b}^x$ in the form $N\left(t\right)=N_o{e}^{kt}$, where $x=t$ and $y=N\left(t\right)$, proceed as follows:

$a{b}^x=N_o{e}^{kt}\left(x=t\right)$

When $x=t=0$, we find $a=N_0$.

This leads to,

$b^x=e^{kt}$

$b^x={\left(e^k\right)}^t$

Therefore, $b=e^k$.

Since, $y=a{b}^x=0.090311284\cdot {\left(1.3384277\right)}^x$; $R^2=0.9927$.

We find that $a=N_0=0.090311284$ and $b=e^k=1.338277$.

Taking log of the equation $b=e^k=1.338277$, we get,

$k=\ln \left(1.338277\right)=0.2915$

As a result, $N\left(t\right)=0.090311284e^{0.2915t}$.

To determine

To answer: The questions based on the given data in the table.

Answer to Problem 1AE

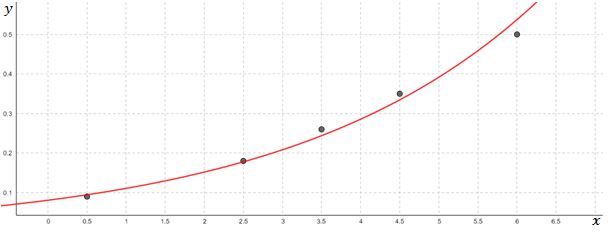
d. Graph.

Explanation of Solution

Given:

Table:

Time (hours), $x$	Population, $y$
0	$0.09$
$2.5$	$0.18$
$3.5$	$0.26$
$4.5$	$0.35$
6	$0.50$

Calculation:

d.

See Figure 2 for the graph of the exponential function of best fit.

To determine

To answer: The questions based on the given data in the table.

Answer to Problem 1AE

e. $y=0.6948$

Explanation of Solution

Given:

Table:

Time (hours), $x$	Population, $y$
0	$0.09$
$2.5$	$0.18$
$3.5$	$0.26$
$4.5$	$0.35$
6	$0.50$

Calculation:

e.

Using the function found in part-b, the population at $x=7$ hours can be predicted as,

$y=0.090311284{\left(1.3384277\right)}^x$

$y=0.6948$

This prediction $(0.6948)$ exceeds the population at 6 hours.

To determine

To answer: The questions based on the given data in the table.

Answer to Problem 1AE

f. After $7.26$ hours.

Explanation of Solution

Given:

Table:

Time (hours), $x$	Population, $y$
0	$0.09$
$2.5$	$0.18$
$3.5$	$0.26$
$4.5$	$0.35$
6	$0.50$

Calculation:

f.

Using the exponential form obtained in part-b, the time at which the population will reach $0.75$ can be obtained as,

$y=0.090311284{\left(1.3384277\right)}^x$

${\left(1.3384277\right)}^x=8.305$

Applying logarithm on both sides,

$\ln 8.305=\ln 1.3384277$

$x=7.26$

Therefore, after $7.26$ hours, the population will reach $0.75$.