Precalculus
Precalculus
17th Edition
ISBN: 9780078035609
Author: Miller, Julie, Gerken, Donna.
Publisher: Mcgraw-hill Education,
bartleby

Concept explainers

Continuous Probability Distributions
Probability distributions are of two types, which are continuous probability distributions and discrete probability distributions. A continuous probability distribution contains an infinite number of values. For example, if time is infinite: you could co…
Normal Distribution
Suppose we had to design a bathroom weighing scale, how would we decide what should be the range of the weighing machine? Would we take the highest recorded human weight in history and use that as the upper limit for our weighing scale? This may not be a…
bartleby

Videos

Textbook Question
Book Icon
Chapter 6, Problem 48RE

For Exercises 47-48, a block is attached to a horizontal spring.

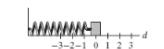
Chapter 6, Problem 48RE, For Exercises 47-48, a block is attached to a horizontal spring. At time t=0 , if the block is

At time t = 0 , if the block is moving to the left with an initial displacement of 0  ft , a maximum displacement of 1 3 and a frequency of 3  Hz , find a model for the displacement d as a function of time t .

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 6, Problem 47RE
Next
Chapter 6, Problem 49RE
Students have asked these similar questions
The period T of a pendulum of length L is T = (2 √L)/√g, where g is the acceleration due to gravity. A pendulum is moved from the Canal Zone, where g = 32.09 feet per second per second, to Greenland, where g = 32.23 feet per second per second. Because of the change in temperature, the length of the pendulum changes from 2.5 feet to 2.48 feet. Approximate the change in the period of the pendulum
The pilot of a jet transport brings the engines to full takeoff before releasing the brakes as the aircraft is standing on the runway. The jet thrust remains constant, and the aircraft has a near-constant acceleration of 0.4g. If the takeoff speed is 200 kph, calculate the distances and time from rest to takeoff.
A hot-air balloon is released at 1:00 P.M. and rises vertically at a rate of 6 m/sec. An observation point is situated 100 meters from a point on the ground directly below the balloon (see the figure). If t denotes the time (in seconds) after 1:00 P.M., use an equation to express the distance d between the balloon and the observation point in terms of t.

Chapter 6 Solutions

Precalculus

Ch. 6.1 - Solve the right triangle. Round the lengths of the...Ch. 6.1 - A 40-ft ladder on a fire truck leans against a...Ch. 6.1 - From an eye level of 6ft , an observer standing...Ch. 6.1 - A straight hiking trail is 2500ft long with a gain...Ch. 6.1 - Prob. 5SPCh. 6.1 - Prob. 6SPCh. 6.1 - A plane leaves an airport heading S50E at 450mph ....Ch. 6.1 - For Exercise 1-2, refer triangle to ABC . If the...Ch. 6.1 - For Exercise 1-2 refer triangle to ABC . The...Ch. 6.1 - Prob. 3PE
Ch. 6.1 - The acute angle used to express the bearing...Ch. 6.1 - For exercise 5-12 given right triangle ABC ,...Ch. 6.1 - For exercise 5-12 given right triangle ABC ,...Ch. 6.1 - For exercise 5-12 given right triangle ABC ,...Ch. 6.1 - For exercise 5-12 given right triangle ABC ,...Ch. 6.1 - For exercise 5-12 given right triangle ABC ,...Ch. 6.1 - For exercise 5-12 given right triangle ABC ,...Ch. 6.1 - Prob. 11PECh. 6.1 - Prob. 12PECh. 6.1 - For Exercises 13-18, solve the right triangle for...Ch. 6.1 - For Exercises 13-18, solve the right triangle for...Ch. 6.1 - For Exercises 13-18, solve the right triangle for...Ch. 6.1 - For Exercises 13-18, solve the right triangle for...Ch. 6.1 - For Exercises 13-18, solve the right triangle for...Ch. 6.1 - For Exercises 13-18, solve the right triangle for...Ch. 6.1 - A boat is anchored off Elliot Key, Florida. From...Ch. 6.1 - A swimming pool has a depth of 4ft at the shallow...Ch. 6.1 - An airplane climbs at an angle of 11 at an average...Ch. 6.1 - An airplane begins its descent with an average...Ch. 6.1 - A railroad bridge over New Scotland Road in...Ch. 6.1 - At 11:30AM. the angle of elevation of the sun for...Ch. 6.1 - Prob. 25PECh. 6.1 - Roberto has plans to build a tree house in a large...Ch. 6.1 - A police officer hiding between two bushes 50 ft...Ch. 6.1 - A large weather balloon is tethered by two ropes....Ch. 6.1 - The Duquesne Incline is a century-old railroad...Ch. 6.1 - The Jackson Hole Aerial Tram takes passengers from...Ch. 6.1 - To approximate the distance from the Earth to...Ch. 6.1 - To approximate the distance from the Earth to...Ch. 6.1 - A sewer line must have a minimum slope of 0.25in....Ch. 6.1 - In order for gravel roads to have proper drainage,...Ch. 6.1 - The weather satellite NOAA-15 orbits the Earth...Ch. 6.1 - A communications satellite is in geosynchronous...Ch. 6.1 - Prob. 37PECh. 6.1 - Prob. 38PECh. 6.1 - Prob. 39PECh. 6.1 - For Exercises 39-42, make a sketch to illustrate...Ch. 6.1 - For Exercises 39-42,, make a sketch to illustrate...Ch. 6.1 - For Exercises 39-42,, make a sketch to illustrate...Ch. 6.1 - For Exercises 43-46, find the bearing of the ship....Ch. 6.1 - For Exercises 43-46, find the bearing of the ship....Ch. 6.1 - For Exercises 43-46, find the bearing of the ship....Ch. 6.1 - For Exercises 43-46, find the bearing of the ship....Ch. 6.1 - For Exercises 47-50, find the bearing to the...Ch. 6.1 - For Exercises 47-50, find the bearing to the...Ch. 6.1 - For Exercises 47-50, find the bearing to the...Ch. 6.1 - For Exercises 47-50, find the bearing to the...Ch. 6.1 - For Exercises 51-54, round answers to the nearest...Ch. 6.1 - Prob. 52PECh. 6.1 - For Exercises 51-54, round answers to the nearest...Ch. 6.1 - For Exercises 51-54, round answers to the nearest...Ch. 6.1 - A ship leaves port at 8 knots heading N27W . After...Ch. 6.1 - Prob. 56PECh. 6.1 - A boat leaves a dock at a bearing of N42W and...Ch. 6.1 - Prob. 58PECh. 6.1 - For Exercises 59-60, find the lengths of the sides...Ch. 6.1 - For Exercises 59-60, find the lengths of the sides...Ch. 6.1 - Find the measures of the sides and angles. Round...Ch. 6.1 - A rectangular prism measures 6in. by 4in. by 3in ....Ch. 6.1 - Two children sit on either end of an 18-ft teeter...Ch. 6.1 - A light fixture mounted 24ft above the ground...Ch. 6.1 - For Exercises 65-66, refer to the table giving the...Ch. 6.1 - For Exercises 65-66, refer to the table giving the...Ch. 6.1 - OSHA safety regulations require that the base of a...Ch. 6.1 - An A-frame storage shed is constructed such that...Ch. 6.1 - An airplane needs to fly to an airfield located...Ch. 6.1 - Software used to program video games often uses an...Ch. 6.1 - Two ships leave port at the same time. One travels...Ch. 6.1 - Prob. 72PECh. 6.1 - Explain how to represent the bearing from point P...Ch. 6.1 - What is meant by solving a triangle?Ch. 6.1 - A contractor building eight ocean-front...Ch. 6.1 - A circle is inscribed within an isosceles triangle...Ch. 6.1 - A tool requires a V-shaped block to hold two...Ch. 6.1 - Pipe for a water line must be installed from a...Ch. 6.1 - A woman participating in a triathlon can run...Ch. 6.2 - Solve ABC with B=70 , C=48, and b=15cm . Round the...Ch. 6.2 - Solve ABC with A=33 , B=112 , and c=16 . Round the...Ch. 6.2 - Solve ABC with A=49 , a=32 , and b=28 . Round the...Ch. 6.2 - Solve ABC with B=31 , b=3 , a=6.2 . Round the...Ch. 6.2 - Solve ABC with A=40 , a=22 , and b=25 . Round the...Ch. 6.2 - A triangle has sides of 12m and 6m , and the angle...Ch. 6.2 - To measures the maximum height of the water in a...Ch. 6.2 - An 80-ft flagpole is located at the top of a hill....Ch. 6.2 - To apply the law of sines, an angle must be given...Ch. 6.2 - In which cases can the law of sines be used to...Ch. 6.2 - Suppose that ABC is a triangle with sides of...Ch. 6.2 - Suppose that the lengths of two sides a and b in a...Ch. 6.2 - Suppose that we know the measure of angle A and...Ch. 6.2 - Suppose that we know the measure of angle A and...Ch. 6.2 - For Exercises 7-12, solve the triangle. For the...Ch. 6.2 - For Exercises 7-12, solve the triangle. For the...Ch. 6.2 - For Exercises 7-12, solve the triangle. For the...Ch. 6.2 - For Exercises 7-12, solve the triangle. For the...Ch. 6.2 - For Exercises 7-12, solve the triangle. For the...Ch. 6.2 - For Exercises 7-12, solve the triangle. For the...Ch. 6.2 - For Exercises 13-20, solve ABC subject to the...Ch. 6.2 - For Exercises 13-20, solve ABC subject to the...Ch. 6.2 - For Exercises 13-20, solve ABC subject to the...Ch. 6.2 - For Exercises 13-20, solve ABC subject to the...Ch. 6.2 - For Exercises 13-20, solve ABC subject to the...Ch. 6.2 - Prob. 18PECh. 6.2 - Prob. 19PECh. 6.2 - For Exercises 13-20, solve ABC subject to the...Ch. 6.2 - For Exercises 21-28, information is given about...Ch. 6.2 - For Exercises 21-28, information is given about...Ch. 6.2 - For Exercises 21-28, information is given about...Ch. 6.2 - For Exercises 21-28, information is given about...Ch. 6.2 - For Exercises 21-28, information is given about...Ch. 6.2 - For Exercises 21-28, information is given about...Ch. 6.2 - For Exercises 21-28, information is given about...Ch. 6.2 - For Exercises 21-28, information is given about...Ch. 6.2 - For Exercises 29-34, find the area of a triangle...Ch. 6.2 - For Exercises 29-34, find the area of a triangle...Ch. 6.2 - For Exercises 29-34, find the area of a triangle...Ch. 6.2 - For Exercises 29-34, find the area of a triangle...Ch. 6.2 - For Exercises 29-34, find the area of a triangle...Ch. 6.2 - For Exercises 29-34, find the area of a triangle...Ch. 6.2 - The area in the Atlantic Ocean known as the...Ch. 6.2 - The triangular face of a gabled roof measures...Ch. 6.2 - Two fire lookout towers at points A and B are 2mi...Ch. 6.2 - A helicopter is on a path directly overhead line...Ch. 6.2 - A surveyor wants to measure the distance across a...Ch. 6.2 - Prob. 40PECh. 6.2 - From a point along a straight road, the angle of...Ch. 6.2 - An observer on the ground sites a plane at an...Ch. 6.2 - A wire is fastened to a point T on a tree and to...Ch. 6.2 - The Leaning Tower of Suurhusen is a medieval...Ch. 6.2 - Prob. 45PECh. 6.2 - A mountain cabin is built on the side of a hill...Ch. 6.2 - Two residential buildings are to be constructed...Ch. 6.2 - A hiker wants to estimate the height of a mountain...Ch. 6.2 - A surveyor fixes a 420-ft baseline between points...Ch. 6.2 - A surveyor fixes a 200-ft baseline between points...Ch. 6.2 - The connector rod from the piston to the...Ch. 6.2 - Two planets follow a circular orbit around a...Ch. 6.2 - For Exercises 53-66, solve ABC . Round the lengths...Ch. 6.2 - For Exercises 53-66, solve ABC . Round the lengths...Ch. 6.2 - For Exercises 53-66, solve ABC . Round the lengths...Ch. 6.2 - For Exercises 53-66, solve ABC . Round the lengths...Ch. 6.2 - For Exercises 53-66, solve ABC . Round the lengths...Ch. 6.2 - For Exercises 53-66, solve ABC . Round the lengths...Ch. 6.2 - For Exercises 53-66, solve ABC . Round the lengths...Ch. 6.2 - For Exercises 53-66, solve ABC . Round the lengths...Ch. 6.2 - For Exercises 53-66, solve ABC . Round the lengths...Ch. 6.2 - For Exercises 53-66, solve ABC . Round the lengths...Ch. 6.2 - For Exercises 53-66, solve ABC . Round the lengths...Ch. 6.2 - For Exercises 53-66, solve ABC . Round the lengths...Ch. 6.2 - For Exercises 53-66, solve ABC . Round the lengths...Ch. 6.2 - For Exercises 53-66, solve ABC . Round the lengths...Ch. 6.2 - After a hurricane, a homeowner examines trees on...Ch. 6.2 - A company manufactures pennants in the shape of an...Ch. 6.2 - Consider a sector of a circle of radius 6cm with...Ch. 6.2 - Refer to the figure. a. Write expressions for the...Ch. 6.2 - Refer to the figure. a. Write expressions for the...Ch. 6.2 - Given ABC with sides of lengths a,b , and c...Ch. 6.2 - Prob. 73PECh. 6.2 - Given SSA (the ambiguous case), outline the four...Ch. 6.2 - List various methods to confirm your answers after...Ch. 6.2 - A triangle ABC has sides a,b , and c across from...Ch. 6.2 - From the figure, show that sin45=23sin95 .Ch. 6.2 - Use the law of sines in the form sinAsinB=ab 1 to...Ch. 6.2 - Use the relationships ac=sinAsinC and bc=sinBsinA...Ch. 6.2 - Given ABC circumscribed by a circle, show that the...Ch. 6.3 - Solve ABC with B=61 , c=19 , and a=28 . Round the...Ch. 6.3 - Solve ABC with a=62 , b=48 , and c=41 . Round the...Ch. 6.3 - Repeat Example 3 with the initial bearing of the...Ch. 6.3 - Find the area of a triangle with sides of length...Ch. 6.3 - In which situation (s) can the law of cosines be...Ch. 6.3 - Given ABC with sides a,b , and c opposite vertices...Ch. 6.3 - Given ABC with sides a,b , and c opposite vertices...Ch. 6.3 - Given a triangle of sides of lengths a,b , and c ,...Ch. 6.3 - For Exercises 5-22, solve ABC subject to the given...Ch. 6.3 - For Exercises 5-22, solve ABC subject to the given...Ch. 6.3 - For Exercises 5-22, solve ABC subject to the given...Ch. 6.3 - For Exercises 5-22, solve ABC subject to the given...Ch. 6.3 - For Exercises 5-22, solve ABC subject to the given...Ch. 6.3 - For Exercises 5-22, solve ABC subject to the given...Ch. 6.3 - For Exercises 5-22, solve ABC subject to the given...Ch. 6.3 - For Exercises 5-22, solve ABC subject to the given...Ch. 6.3 - For Exercises 5-22, solve ABC subject to the given...Ch. 6.3 - For Exercises 5-22, solve ABC subject to the given...Ch. 6.3 - For Exercises 5-22, solve ABC subject to the given...Ch. 6.3 - For Exercises 5-22, solve ABC subject to the given...Ch. 6.3 - Prob. 17PECh. 6.3 - For Exercises 5-22, solve ABC subject to the given...Ch. 6.3 - For Exercises 5-22, solve ABC subject to the given...Ch. 6.3 - For Exercises 5-22, solve ABC subject to the given...Ch. 6.3 - Prob. 21PECh. 6.3 - For Exercises 5-22, solve ABC subject to the given...Ch. 6.3 - A boat leaves port and follows a course of N77E at...Ch. 6.3 - A fishing boat leaves a marina and follows a...Ch. 6.3 - Two planes leave the same airport. The first plane...Ch. 6.3 - Two boats leave a marina at the same time. The...Ch. 6.3 - A 40-ft boom on a crane is attached to the crane...Ch. 6.3 - Prob. 28PECh. 6.3 - A regulation fast-pitch softball diamond for high...Ch. 6.3 - The Flatiron Building in New York City is said to...Ch. 6.3 - The distance between Dallas, Texas, and Atlanta,...Ch. 6.3 - A bicyclist is at point A on a paved road and must...Ch. 6.3 - A 150-ft tower is anchored on a hill by two guy...Ch. 6.3 - A 75-ft tower is located on the side of a hill...Ch. 6.3 - In Exercises 35-38, use Heron's formula to find...Ch. 6.3 - In Exercises 35-38, use Heron's formula to find...Ch. 6.3 - In Exercises 35-38, use Heron's formula to find...Ch. 6.3 - In Exercises 35-38, use Heron's formula to find...Ch. 6.3 - A triangular sail for a Bolger Tortise sailboat...Ch. 6.3 - Find the area of the grassy region from Exercise...Ch. 6.3 - A farmer wants to fertilize a triangular field...Ch. 6.3 - An artist lays down a white triangular background...Ch. 6.3 - For Exercises 43-46, the vertices of a triangle...Ch. 6.3 - For Exercises 43-46, the vertices of a triangle...Ch. 6.3 - For Exercises 43-46, the vertices of a triangle...Ch. 6.3 - For Exercises 43-46, the vertices of a triangle...Ch. 6.3 - Three mutually tangential circles with radii...Ch. 6.3 - Prob. 48PECh. 6.3 - A parallelogram has adjacent sides of 12.2cm and...Ch. 6.3 - A regular octagon (8- sided figure with sides of...Ch. 6.3 - Why is the law of sines not an option to solve a...Ch. 6.3 - To solve a triangle given SAS , the law of cosines...Ch. 6.3 - Given the lengths of the three sides of a triangle...Ch. 6.3 - When applying the law of cosines (or law of sines)...Ch. 6.3 - Suppose that ABC is a right triangle with right...Ch. 6.3 - If the measures of the three angles in a triangle...Ch. 6.3 - A piston in an engine is attached to a connector...Ch. 6.3 - Use the law of cosines to show that...Ch. 6.3 - Use the law of cosines to show that a=bcosC+ccosBCh. 6.3 - Prob. 60PECh. 6.3 - For Exercises 1-12, solve ABC subject to the given...Ch. 6.3 - For Exercises 1-12, solve ABC subject to the given...Ch. 6.3 - For Exercises 1-12, solve ABC subject to the given...Ch. 6.3 - For Exercises 1-12, solve ABC subject to the given...Ch. 6.3 - For Exercises 1-12, solve ABC subject to the given...Ch. 6.3 - For Exercises 1-12, solve ABC subject to the given...Ch. 6.3 - For Exercises 1-12, solve ABC subject to the given...Ch. 6.3 - For Exercises 1-12, solve ABC subject to the given...Ch. 6.3 - For Exercises 1-12, solve ABC subject to the given...Ch. 6.3 - For Exercises 1-12, solve ABC subject to the given...Ch. 6.3 - For Exercises 1-12, solve ABC subject to the given...Ch. 6.3 - For Exercises 1-12, solve ABC subject to the given...Ch. 6.3 - Refer to the figure. Find the indicated values to...Ch. 6.3 - Use the right triangles APB and APC to show that...Ch. 6.3 - A hiking trail is roughly in the shape of a circle...Ch. 6.4 - Suppose the block from Example 1 is initially...Ch. 6.4 - Repeat Example 2 with a Ferris wheel 120ft in...Ch. 6.4 - Two spring-mass systems have an initial...Ch. 6.4 - The of an object in simple harmonic motion is the...Ch. 6.4 - For an object in simple harmonic motion, the...Ch. 6.4 - Given an object in damped harmonic motion, the...Ch. 6.4 - The term "ultrasound" refers to sound waves of a...Ch. 6.4 - The frequency of middle C on a piano is. 264Hz ....Ch. 6.4 - If the displacement d of an object moving under...Ch. 6.4 - For Exercises 7-14, suppose that an object moves...Ch. 6.4 - For Exercises 7-14, suppose that an object moves...Ch. 6.4 - For Exercises 7-14, suppose that an object moves...Ch. 6.4 - For Exercises 7-14, suppose that an object moves...Ch. 6.4 - For Exercises 7-14, suppose that an object moves...Ch. 6.4 - For Exercises 7-14, suppose that an object moves...Ch. 6.4 - For Exercises 7-14, suppose that an object moves...Ch. 6.4 - For Exercises 7-14, suppose that an object moves...Ch. 6.4 - For Exercises 15-22, suppose that an object is...Ch. 6.4 - For Exercises 15-22, suppose that an object is...Ch. 6.4 - Prob. 17PECh. 6.4 - For Exercises 15-22, suppose that an object is...Ch. 6.4 - For Exercises 15-22, suppose that an object is...Ch. 6.4 - For Exercises 15-22, suppose that an object is...Ch. 6.4 - For Exercises 15-22, suppose that an object is...Ch. 6.4 - For Exercises 15-22, suppose that an object is...Ch. 6.4 - A block hangs on a spring attached to the ceiling...Ch. 6.4 - The bob on a simple pendulum is pulled to the left...Ch. 6.4 - Prob. 25PECh. 6.4 - The blood pressure p for a certain individual...Ch. 6.4 - A Ferris wheel at a county Fair is 180ft in...Ch. 6.4 - The 30-ft diameter waterwheel at Deleon Springs...Ch. 6.4 - Refer to the piston and crankshaft from Exercise...Ch. 6.4 - A laboratory centrifuge is a piece of equipment...Ch. 6.4 - An alternating current generator generates current...Ch. 6.4 - An alternating current generator in the United...Ch. 6.4 - Prob. 33PECh. 6.4 - Prob. 34PECh. 6.4 - The brightness of a "young" star sometimes...Ch. 6.4 - The magnitude of a star named Delta Cuphea varies...Ch. 6.4 - For Exercises 37-38, the ordered pair t,d gives...Ch. 6.4 - For Exercises 37-38, the ordered pair t,d gives...Ch. 6.4 - Write a function y=ft for simple harmonic motion...Ch. 6.4 - Write a function y=ft for simple harmonic motion...Ch. 6.4 - Use a graphing utility to graph the functions of...Ch. 6.4 - Prob. 42PECh. 6.4 - Prob. 43PECh. 6.4 - For Exercises 43-46, use a graphing utility to...Ch. 6.4 - For Exercises 43-46, use a graphing utility to...Ch. 6.4 - For Exercises 43-46, use a graphing utility to...Ch. 6.4 - Suppose that a guitar string is plucked such that...Ch. 6.4 - A tuning fork is struck, and the tips of the...Ch. 6.4 - Explain the criteria under which you would choose...Ch. 6.4 - Explain the difference between an object moving in...Ch. 6.4 - Prob. 51PECh. 6.4 - Prob. 52PECh. 6.4 - Prob. 53PECh. 6.4 - For Exercises 53-54, use the model d=aectcost or...Ch. 6.4 - In a course in differential equations or physics,...Ch. 6.4 - In a course in differential equations or physics,...Ch. 6.4 - Given the model d2006tcos2t . for an object in...Ch. 6.4 - Given the model d=804tcost for an object in damped...Ch. 6.4 - Given a point on the Earth of latitude a, the...Ch. 6.4 - Given a point on the Earth of latitude a, the...Ch. 6 - For Exercises 1-4, solve the right triangle for...Ch. 6 - Prob. 2RECh. 6 - For Exercises 1-4, solve the right triangle for...Ch. 6 - For Exercises 1-4, solve the right triangle for...Ch. 6 - A 20-ft-tall light post casts a 25-ft shadow along...Ch. 6 - A passenger lift runs 680ft up the side of a...Ch. 6 - A 75-ft guy wire is attached to the top of a...Ch. 6 - A 125-ft kite string is anchored to the ground. If...Ch. 6 - Prob. 9RECh. 6 - Prob. 10RECh. 6 - A plane flies due west for 2hr then due south for...Ch. 6 - A boat travels 3mi east then 7mi south. To the...Ch. 6 - A ship leaves a dock on a bearing of S48.2W ....Ch. 6 - A plane flying 275mph on a bearing of N73.5W...Ch. 6 - For Exercises 15-20, solve ABC subject to the...Ch. 6 - Prob. 16RECh. 6 - For Exercises 15-20, solve ABC subject to the...Ch. 6 - Prob. 18RECh. 6 - Prob. 19RECh. 6 - Prob. 20RECh. 6 - For Exercises 21-22, find the area of a triangle...Ch. 6 - Prob. 22RECh. 6 - Points on a straight shoreline, A and B , are...Ch. 6 - Two landing points, A and B , lie on the straight...Ch. 6 - A ranger station at a point R in a wilderness area...Ch. 6 - Standing on top of a 30-ft lifeguard tower, an...Ch. 6 - PointsA,B, and P are collinear points along a...Ch. 6 - A surveyor fixes a baseline of 64 ft between two...Ch. 6 - For Exercises 29-32, solve ABC subject to the...Ch. 6 - Prob. 30RECh. 6 - For Exercises 29-32, solve ABC subject to the...Ch. 6 - Prob. 32RECh. 6 - For Exercises 33-34, find the measures of the...Ch. 6 - Prob. 34RECh. 6 - Prob. 35RECh. 6 - In Exercises 35-36, find the area of the triangle...Ch. 6 - Two straight jogging paths begin at a kiosk in a...Ch. 6 - Given points A6,2 and B1,4 on the coordinate...Ch. 6 - Prob. 39RECh. 6 - Two planes take off from an airport at the same...Ch. 6 - Two sides of a triangular plot of land measure...Ch. 6 - Prob. 42RECh. 6 - For Exercises 43-46, suppose that an object moves...Ch. 6 - Prob. 44RECh. 6 - For Exercises 43-46, suppose that an object moves...Ch. 6 - Prob. 46RECh. 6 - Prob. 47RECh. 6 - For Exercises 47-48, a block is attached to a...Ch. 6 - The angular displacement (in radians) for a...Ch. 6 - A Ferris wheel is 200ft in diameter with its...Ch. 6 - For Exercises 51-52, use a graphing utility to...Ch. 6 - For Exercises 51-52, use a graphing utility to...Ch. 6 - For Exercises 1-8, solve ABC subject to the given...Ch. 6 - For Exercises 1-8, solve ABC subject to the given...Ch. 6 - For Exercises 1-8, solve ABC subject to the given...Ch. 6 - For Exercises 1-8, solve ABC subject to the given...Ch. 6 - Prob. 5TCh. 6 - Prob. 6TCh. 6 - For Exercises 1-8, solve ABC subject to the given...Ch. 6 - Prob. 8TCh. 6 - Prob. 9TCh. 6 - Prob. 10TCh. 6 - For Exercises 9-12, find the area of ABC with the...Ch. 6 - Prob. 12TCh. 6 - A ship travels west at 25 knots. At 7:30P.M. , the...Ch. 6 - Over the course of a day, as the angle of...Ch. 6 - To determine the height of a tower, a surveyor...Ch. 6 - In addition to the light-year to quantify large...Ch. 6 - A triangular shade sail has sides of length 123...Ch. 6 - The distance between Los Angeles, California, and...Ch. 6 - The connector rod from the piston to the...Ch. 6 - Prob. 20TCh. 6 - Prob. 21TCh. 6 - The displacement of an object attached to a spring...Ch. 6 - Prob. 23TCh. 6 - A block hangs on a spring attached to the ceiling...Ch. 6 - The angular displacement (in radians) for a...Ch. 6 - Prob. 26TCh. 6 - Use a graphing utility to graph the function...Ch. 6 - Write the equation of the line in slope-intercept...Ch. 6 - Prob. 2CRECh. 6 - Prob. 3CRECh. 6 - Write a polynomial fx of degree 5 , with integer...Ch. 6 - Write equations for the asymptotes for the graph...Ch. 6 - Write equations for the asymptotes for the graph...Ch. 6 - Prob. 7CRECh. 6 - Prob. 8CRECh. 6 - Write an equation for a tangent function with a...Ch. 6 - A motorist drives on a toll road to and from work...Ch. 6 - a. Write a variation model using k as the constant...Ch. 6 - a. Write an equation representing the fact that...Ch. 6 - Prob. 13CRECh. 6 - The cost to buy tickets to a concert is $50 per...Ch. 6 - Suppose that the population of a country in the...Ch. 6 - Prob. 16CRECh. 6 - Prob. 17CRECh. 6 - Find the exact value of cos200cos50+sin200sin50Ch. 6 - Prob. 19CRECh. 6 - For Exercises 19-20, solve ABC subject to the...

Additional Math Textbook Solutions

Find more solutions based on key concepts
In Problems 19-26, sketch the graph of each function. Be sure to label three points on the graph. f( x )= 1 x

Precalculus (10th Edition)

The graphs of force functions (in newtons) are given in Exercises 1 and 2. How much work is done by each force ...

University Calculus: Early Transcendentals (4th Edition)

The value of dydx .

Calculus: Early Transcendentals (3rd Edition)

Moving shadow A 5-foot-tall woman walks at 8 ft/s toward a streetlight that is 20 ft above the ground. What is ...

Single Variable Calculus: Early Transcendentals (2nd Edition) - Standalone book

In Problems , find the domain of each function.

Precalculus

Evaluate the integrals in Exercise 1–22. 1.

Thomas' Calculus: Early Transcendentals (14th Edition)

Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
College Algebra
Algebra
ISBN:9781337282291
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Text book image
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
SEE MORE TEXTBOOKS
Continuous Probability Distributions - Basic Introduction; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=QxqxdQ_g2uw;License: Standard YouTube License, CC-BY
Probability Density Function (p.d.f.) Finding k (Part 1) | ExamSolutions; Author: ExamSolutions;https://www.youtube.com/watch?v=RsuS2ehsTDM;License: Standard YouTube License, CC-BY
Find the value of k so that the Function is a Probability Density Function; Author: The Math Sorcerer;https://www.youtube.com/watch?v=QqoCZWrVnbA;License: Standard Youtube License