Mathematics For Machine Technology
8th Edition
ISBN: 9781337798310
Author: Peterson, John.
Publisher: Cengage Learning,
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 59, Problem 1A
Trace this line segment two times. On one copy construct a perpendicular bisector of the segment. On the other copy divide the segment into three equal segments.
Expert Solution & Answer
To determine
To construct:
A perpendicular bisector of the line segment.
To divide: The line segment into three equal parts.
Answer to Problem 1A
Area
Explanation of Solution
Steps of construction:
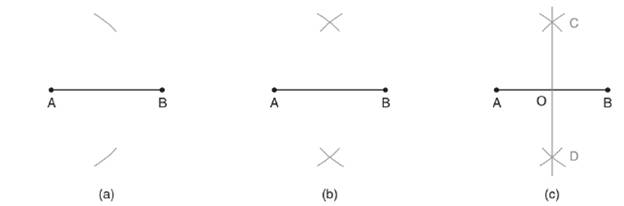
- Taking A as a centre and radius more than half of AB, draw arcs on both the above and below the line segment AB as shown in figure (a).
- Similarly, taking B as a centre and radius same as above draw another arc on both the sides of the line segment that intersects the first pair of arcs as shown in the diagram (b).
- Join both the arcs by drawing a straight line. Line CD as shown in figure (c), is the perpendicular bisector of line segment AB with O as a centre.
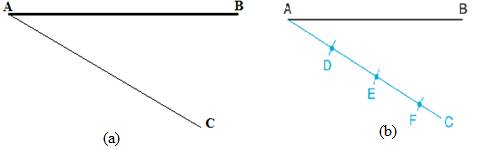
Divide the line segment into three equal parts:
Steps of construction:
- From point A, draw a line segment AC forming an angle with AB as shown in fig(a).
- On line segment AC with the help of a compass mark three equal arcs D, E and F of any length (b).
- Connect point F with point B.
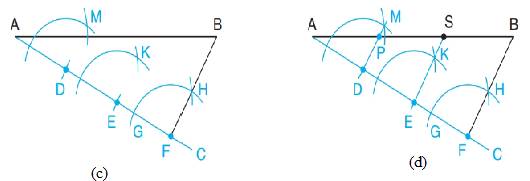
- Now taking F as a centre, draw arcs which intersect the line segment AC at G and BF at H.
- Repeat the procedure by taking D and E as centre and mark an arc of same radii as shown in figure.
- With the help of a compass measure the distance GH and mark the same distance from other two arcs as well which intersects the arcs at point K and M respectively.
- Join E with K and D with M and extending the lines past AB. Thus, line segment AB is divided into three equal parts.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
Can you help me with this problem using linear recurrance: Find an explicit formula for the recurrence relation an = 2can−1 + 3c2an−2 where c not equal to 0 with initial conditions a0=4c and a1 = 0
Can you help me solved this problem using generalized combination:How many combinations are there to pick r objects from 2n objects numbered from 1to 2n when repetitions are allowed and at least one object of odd type does not appear?
N
Chapter 59 Solutions
Mathematics For Machine Technology
Ch. 59 - Trace this line segment two times. On one copy...Ch. 59 - Find the length of x. Round the answer to 2...Ch. 59 - Prob. 3ACh. 59 - Prob. 4ACh. 59 - Prob. 5ACh. 59 - Prob. 6ACh. 59 - Prob. 7ACh. 59 - Prob. 8ACh. 59 - Prob. 9ACh. 59 - Prob. 10A
Ch. 59 - Prob. 11ACh. 59 - Prob. 12ACh. 59 - Prob. 13ACh. 59 - Express each area as indicated. Round each answer...Ch. 59 - Prob. 15ACh. 59 - Prob. 16ACh. 59 - Prob. 17ACh. 59 - Prob. 18ACh. 59 - Prob. 19ACh. 59 - Prob. 20ACh. 59 - Prob. 21ACh. 59 - Prob. 22ACh. 59 - Prob. 23ACh. 59 - Prob. 24ACh. 59 - Prob. 25ACh. 59 - Prob. 26ACh. 59 - Prob. 27ACh. 59 - Prob. 28ACh. 59 - Prob. 29ACh. 59 - Prob. 30ACh. 59 - Prob. 31ACh. 59 - Prob. 32ACh. 59 - Prob. 33ACh. 59 - Prob. 34ACh. 59 - Prob. 35ACh. 59 - Prob. 36ACh. 59 - Prob. 37ACh. 59 - Prob. 38ACh. 59 - Prob. 39ACh. 59 - Prob. 40ACh. 59 - Prob. 41ACh. 59 - Prob. 42ACh. 59 - Prob. 43ACh. 59 - Prob. 44ACh. 59 - Prob. 45ACh. 59 - Prob. 46ACh. 59 - Prob. 47ACh. 59 - Prob. 48ACh. 59 - Prob. 49ACh. 59 - Prob. 50ACh. 59 - Prob. 51ACh. 59 - Prob. 52ACh. 59 - Prob. 53ACh. 59 - Prob. 54ACh. 59 - Prob. 55ACh. 59 - Prob. 56ACh. 59 - Prob. 57ACh. 59 - Prob. 58ACh. 59 - Prob. 59ACh. 59 - Prob. 60ACh. 59 - Prob. 61ACh. 59 - Prob. 62ACh. 59 - Prob. 63ACh. 59 - Prob. 64ACh. 59 - Prob. 65ACh. 59 - Prob. 66ACh. 59 - Prob. 67ACh. 59 - Prob. 68ACh. 59 - Prob. 69ACh. 59 - Prob. 70ACh. 59 - Prob. 71ACh. 59 - Prob. 72ACh. 59 - Prob. 73ACh. 59 - Prob. 74ACh. 59 - Find the unknown area, height, or base for each of...Ch. 59 - Find the unknown area, height, or base for each of...Ch. 59 - A cross section of an aluminum bar in the shape of...Ch. 59 - Prob. 78ACh. 59 - Prob. 79ACh. 59 - One of the examples showed how to find the area of...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Please help me organize the proof of the following theorem:arrow_forwardHow come that I marked ?arrow_forwardIn Exercises 1-14, state whether each statement is true or false. If false, give a reason. 1. The set of stores located in the state of Wyoming is a well- defined set. 2. The set of the three best songs is a well-defined set. 3. maple = {oak, elm, maple, sycamore} 4{} cơ 5. {3, 6, 9, 12,...} and {2, 4, 6, 8, ...} are disjoint sets. 6. {Mercury, Venus, Earth, Mars} is an example of a set in roster form. 7. {candle, picture, lamp} = {picture, chair, lamp } 8. {apple, orange, banana, pear} is equivalent to {tomato, corn, spinach, radish}.arrow_forward
- Exercises Evaluate the following limits. 1. lim cot x/ln x +01x 2. lim x² In x +014 3. lim x* x0+ 4. lim (cos√√x)1/x +014 5. lim x2/(1-cos x) x10 6. lim e*/* 818 7. lim (secx - tan x) x-x/2- 8. lim [1+(3/x)]* x→∞0arrow_forwardIn Exercises 1 through 3, let xo = O and calculate P7(x) and R7(x). 1. f(x)=sin x, x in R. 2. f(x) = cos x, x in R. 3. f(x) = In(1+x), x≥0. 4. In Exercises 1, 2, and 3, for |x| 1, calculate a value of n such that P(x) approximates f(x) to within 10-6. 5. Let (an)neN be a sequence of positive real numbers such that L = lim (an+1/an) exists in R. If L < 1, show that an → 0. [Hint: Let 1111 Larrow_forwardiation 7. Let f be continuous on [a, b] and differentiable on (a, b). If lim f'(x) xia exists in R, show that f is differentiable at a and f'(a) = lim f'(x). A similar result holds for b. x-a 8. In reference to Corollary 5.4, give an example of a uniformly continuous function on [0, 1] that is differentiable on (0, 1] but whose derivative is not bounded there. 9. Recall that a fixed point of a function f is a point c such that f(c) = c. (a) Show that if f is differentiable on R and f'(x)| x if x 1 and hence In(1+x) 0. 12. For 0 л/2. (Thus, as x л/2 from the left, cos x is never large enough for x+cosx to be greater than л/2 and cot x is never small enough for x + cot x to be less than x/2.)arrow_forward1. Show that f(x) = x3 is not uniformly continuous on R. 2. Show that f(x) = 1/(x-2) is not uniformly continuous on (2,00). 3. Show that f(x)=sin(1/x) is not uniformly continuous on (0,л/2]. 4. Show that f(x) = mx + b is uniformly continuous on R. 5. Show that f(x) = 1/x2 is uniformly continuous on [1, 00), but not on (0, 1]. 6. Show that if f is uniformly continuous on [a, b] and uniformly continuous on D (where D is either [b, c] or [b, 00)), then f is uniformly continuous on [a, b]U D. 7. Show that f(x)=√x is uniformly continuous on [1, 00). Use Exercise 6 to conclude that f is uniformly continuous on [0, ∞). 8. Show that if D is bounded and f is uniformly continuous on D, then fis bounded on D. 9. Let f and g be uniformly continuous on D. Show that f+g is uniformly continuous on D. Show, by example, that fg need not be uniformly con- tinuous on D. 10. Complete the proof of Theorem 4.7. 11. Give an example of a continuous function on Q that cannot be continuously extended to R. 12.…arrow_forwardcan I see the steps for how you got the same answers already provided for μ1->μ4. this is a homework that provide you answers for question after attempting it three triesarrow_forward1. Prove that for each n in N, 1+2++ n = n(n+1)/2. 2. Prove that for each n in N, 13 +23+ 3. Prove that for each n in N, 1+3+5+1 4. Prove that for each n ≥ 4,2" -1, then (1+x)" ≥1+nx for each n in N. 11. Prove DeMoivre's Theorem: fort a real number, (cost+i sint)" = cos nt + i sinnt for each n in N, where i = √√-1.arrow_forwardPls help ASAParrow_forward2. Sam and Deb have a weekly net income of $1500. They have a pet dog. Their monthly expenses, not related to housing, are $2875. They have savings of $32 000. They are considering two housing options: Option 1: Renting a 2-bedroom condo for $1650 a month, plus utilities averaging $210 a month Option 2: Buying a 2-bedroom condo for a down payment of $24 500, bi-weekly mortgage payments of $1100, and a monthly condo fee of $475 a) Determine the monthly cost of each housing option. Factoring in other expenses not related to housing, which one can Sam and Deb afford? b) Suppose their dog falls ill and they have to pay $85 every week to cover veterinarian and medical expenses. Calculate the additional monthly expenses. How much money would be available for savings if they choose housing option 2?arrow_forwardI bought sparrows at 3 for a penny, turtle doves at 2 for a penny, anddoves at 2 pence each. If I spent 30 pence buying 30 birds and boughtat least one of each kind of bird, how many birds of each kind did I buy?(This is a problem from Fibonacci’s Liber Abaci, 1202.)arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Elementary Algebra
Algebra
ISBN:9780998625713
Author:Lynn Marecek, MaryAnne Anthony-Smith
Publisher:OpenStax - Rice University
Points, Lines, Planes, Segments, & Rays - Collinear vs Coplanar Points - Geometry; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=dDWjhRfBsKM;License: Standard YouTube License, CC-BY
Naming Points, Lines, and Planes; Author: Florida PASS Program;https://www.youtube.com/watch?v=F-LxiLSSaLg;License: Standard YouTube License, CC-BY