HEART OF MATHEMATICS
4th Edition
ISBN: 9781119760061
Author: Burger
Publisher: WILEY
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5.1, Problem 23MS
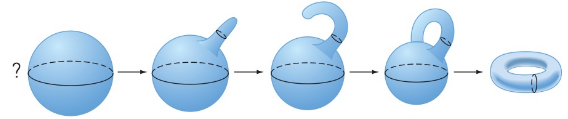
From sphere to torus. The following sequence of drawings takes a sphere and deforms it into a torus. Does this sequence desribe an equivalence by distortion? Why or why not?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
8.64 Radon exposure in Egyptian tombs. Refer to the
D Radiation Protection Dosimetry (Dec. 2010) study
TOMBS of radon exposure in Egyptian tombs, Exercise 7.39
(p. 334). The radon levels-measured in becquerels per
cubic meter (Bq/m³)-in the inner chambers of a sam-
ple of 12 tombs are listed in the table. For the safety of
the guards and visitors, the Egypt Tourism Authority
(ETA) will temporarily close the tombs if the true mean
level of radon exposure in the tombs rises to 6,000 Bq/m³.
Consequently, the ETA wants to conduct a test to deter-
mine if the true mean level of radon exposure in the tombs
is less than 6,000 Bq/m³, using a Type I error probabil-
ity of .10. A SAS analysis of the data is shown on p. 399.
Specify all the elements of the test: Ho, Ha, test statistic,
p-value, a, and your conclusion.
50
390
910
12100
180
580
7800
4000
3400
1300
11900 1100
N Mean Std Dev Std Err Minimum Maximum
12 3642.5
4486.9 1295.3
50.0000
12100.0
Reduction in the particle size of a drug in a solid dosage form results in its faster dissolution. Please select one of the following correct option with respect to this statement
A. Yes because reduction in size results in decrease in surface area
B. Yes because reduction in size results in increase in surface area
C. The above statement is incorrect because rate of dissolution, in fact, decreases with decrease in particle size of the drug
__ Only B is correct
__ Only C is correct
__ Only A is correct
Show all steps. Correct answer is 37.6991118
Chapter 5 Solutions
HEART OF MATHEMATICS
Ch. 5.1 - Describing distortion. What does it mean to say...Ch. 5.1 - Your last sheet. Youre in your bathroom reading...Ch. 5.1 - Rubber polygons. Find a large rubber band and...Ch. 5.1 - Out, out red spot. Remove the red spot from the...Ch. 5.1 - That theta (S). Does there exist a pair of points...Ch. 5.1 - Your ABCs (H). Consider the following letters made...Ch. 5.1 - Half dollar and a straw. Suppose we drill a hole...Ch. 5.1 - Drop them. Is it possible to take off your...Ch. 5.1 - Coffee and doughnuts (H). Is a standard coffee mug...Ch. 5.1 - Lasting ties. Tie a thin rope around a friends...
Ch. 5.1 - Will you spill? (S). Suppose you rest a glass of...Ch. 5.1 - Grabbing the brass ring. Suppose a string attached...Ch. 5.1 - Hair care. Is a regular comb equivalent by...Ch. 5.1 - Three two-folds. Take three pieces of paper and...Ch. 5.1 - Equivalent objects. Group the objects in this...Ch. 5.1 - Clips. Is a paper clip equivalent to a circle? If...Ch. 5.1 - Pennies plus. Consider the two objects pictured...Ch. 5.1 - Starry-eyed. Consider the two stars below. Are...Ch. 5.1 - Learning the ropes. Pictured below are two ropes,...Ch. 5.1 - HoIy spheres. Consider the two spheres shown. Each...Ch. 5.1 - From sphere to torus. The following sequence of...Ch. 5.1 - Half full, half empty. One glass is half filled...Ch. 5.1 - Male versus female. Consider the male and female...Ch. 5.1 - Holey tori. Are these two objects equivalent by...Ch. 5.1 - More holey tori (H). Are these two objects...Ch. 5.1 - Last holey tori. Are these two objects equivalent...Ch. 5.1 - Beyond the holey inner tube. Suppose you are given...Ch. 5.1 - Heavy metal. Carefully examine this picture of a...Ch. 5.1 - The disk and the inner tube (ExH). Suppose you...Ch. 5.1 - Building a torus (S). Suppose you are given a...Ch. 5.1 - Lasso that hole. Consider the first two tori on...Ch. 5.1 - Knots in dougtnuts. We are given two solid...Ch. 5.1 - From knots to glasses (ExH). Take the thickened...Ch. 5.1 - More Jell-O. Suppose we take a cube of Jell-O,...Ch. 5.1 - Fixed spheres (H). We are given two spheres made...Ch. 5.1 - Holes. Is a torus equivalent to a two-holed torus?...Ch. 5.1 - More holes. Is a two-holed torus equivalent to a...Ch. 5.1 - Here we celebrate the power of algebra as a...Ch. 5.1 - Here we celebrate the power of algebra as a...Ch. 5.1 - Here we celebrate the power of algebra as a...Ch. 5.1 - Here we celebrate the power of algebra as a...Ch. 5.1 - Here we celebrate the power of algebra as a...Ch. 5.2 - One side to every story. What is a Mobius band?Ch. 5.2 - Maybe Mobius. How can you look at a loop of paper...Ch. 5.2 - Singin the blues. Take an ordinary strip of white...Ch. 5.2 - Whos blue now? Take an ordinary strip of white...Ch. 5.2 - Twisted sister. Your sister holds a strip of...Ch. 5.2 - Two twists. Take a strip of paper, put two half...Ch. 5.2 - Two twists again. Take a strip of paper, put two...Ch. 5.2 - Three twists (H). Take a strip of paper, put three...Ch. 5.2 - Prob. 11MSCh. 5.2 - Möbius lengths. Use the edge identification...Ch. 5.2 - Squash and cut. Take a Möbius band and squash it...Ch. 5.2 - Two at once. Take two strips of paper and put them...Ch. 5.2 - Parallel Möbius. Is it possible to have two...Ch. 5.2 - Puzzling. Suppose you have a collection of jigsaw...Ch. 5.2 - Möbius triangle. Make a 1-inch-wide Möbius band,...Ch. 5.2 - Thickened Möbius. Imagine a Möbius band...Ch. 5.2 - Thickened faces. How many faces (sides) does a...Ch. 5.2 - Thick then thin. Suppose we take a Môbius band,...Ch. 5.2 - Drawing the band (ExH). Imagine you have a Möbius...Ch. 5.2 - Tubing (H). Suppose we take two Möbius bands and...Ch. 5.2 - Bug out (ExH). Suppose you are a ladybug on the...Ch. 5.2 - Open cider. Consider the Klein bottle half filled...Ch. 5.2 - Rubber Klein (S). Suppose you have a rectangular...Ch. 5.2 - One edge. Using the method on page 347 for...Ch. 5.2 - Twist of fate (S). Using the edge-identification...Ch. 5.2 - Linked together. Using the edge-identification...Ch. 5.2 - Count twists. Using the edge-identification...Ch. 5.2 - Dont cross. Can you draw a curve that does not...Ch. 5.2 - Twisted up (H). Suppose you are given a band of...Ch. 5.2 - Prob. 32MSCh. 5.2 - Find a band. Find a Möbius band on the surface of...Ch. 5.2 - Holy Klein. Show that the figure on the left is...Ch. 5.2 - Möbius Möbius. Show that the Klein bottle is two...Ch. 5.2 - Attaching tubes. Consider a Möbius band with two...Ch. 5.2 - Möbius map (H). Using felt-tip color pens that...Ch. 5.2 - Thick slices. Thicken a Môbius band and then...Ch. 5.2 - Bagel slices. If we take a bagel and slice it in...Ch. 5.2 - Gluing and cutting. Consider a rectangular sheet...Ch. 5.2 - Here we celebrate the power of algebra as a...Ch. 5.2 - Here we celebrate the power of algebra as a...Ch. 5.2 - Here we celebrate the power of algebra as a...Ch. 5.2 - Here we celebrate the power of algebra as a...Ch. 5.2 - Here we celebrate the power of algebra as a...Ch. 5.3 - Knotty start. Which of the followign knots are...Ch. 5.3 - The not knot. What is the unknot?Ch. 5.3 - Crossing count. Count the crossings in each knot...Ch. 5.3 - Tangled up. Is the figure below a knot or a link?Ch. 5.3 - Ringing endorsement. What are the Borromean rings?Ch. 5.3 - Human trefoil. What is the minimum number of...Ch. 5.3 - Human figure eight. What is the minimum number of...Ch. 5.3 - Stick number (ExH). What is the smallest number...Ch. 5.3 - More Möbius. Make a Möbius band with three half...Ch. 5.3 - Slinky (H). Take a Slinky, lengthen one of its...Ch. 5.3 - More slink. Take a Slinky, and this time weave an...Ch. 5.3 - Make it. Use a piece of string or an extenstion...Ch. 5.3 - Knotted (S). Take an unknotted loop. Tie a knot in...Ch. 5.3 - Slip. Take an unknotted loop and put a slip knot...Ch. 5.3 - Dollar link. Take two paper clips and a dollar and...Ch. 5.3 - Prob. 18MSCh. 5.3 - Unknotting knots (H). In each of the two knots at...Ch. 5.3 - Alternating. A picture of a knot is alternating...Ch. 5.3 - Making it alternating. Consider the knot on the...Ch. 5.3 - Prob. 22MSCh. 5.3 - One cross (H). Prove that any loop with exactly...Ch. 5.3 - Two loops (S). Is there a picture of two linked...Ch. 5.3 - Hold the phone. Disconnect the wire from the phone...Ch. 5.3 - More unknotting knots. In these two knots, find...Ch. 5.3 - Unknotting pictures (S). Suppose you are given a...Ch. 5.3 - Twisted. Suppose we are given a figure consisting...Ch. 5.3 - More alternating. First reread Mindscape 20. For...Ch. 5.3 - Crossing numbers. Suppose you are given pictures...Ch. 5.3 - Lots of crossings. Suppose you arc given a picture...Ch. 5.3 - Torus knots (H). Can you draw a trefoil knot on a...Ch. 5.3 - Two crosses. Prove that any loop with exactly two...Ch. 5.3 - Hoop it up. Show that every knot can be positioned...Ch. 5.3 - The switcheroo. Pictured below is a way of...Ch. 5.3 - 4D washout. Why is the study of knots and links...Ch. 5.3 - Brunnian links (H). Link four loops together in...Ch. 5.3 - Fire drill (ExH). A fire starts in your...Ch. 5.3 - Fixed spheres again. We are given two spheres that...Ch. 5.3 - Here we celebrate the power of algebra as a...Ch. 5.3 - Here we celebrate the power of algebra as a...Ch. 5.3 - Here we celebrate the power of algebra as a...Ch. 5.3 - Here we celebrate the power of algebra as a...Ch. 5.3 - Here we celebrate the power of algebra as a...Ch. 5.4 - Fixed things first. What does the Brouwer Fixed...Ch. 5.4 - Say cheese. Youre making an open-faced cheese...Ch. 5.4 - Fixed flapjacks. Youre making pancakes and...Ch. 5.4 - Prob. 4MSCh. 5.4 - Loop around. What does the Hot Loop Theorem...Ch. 5.4 - Fixed on a square. Does the Brouwer Fixed Point...Ch. 5.4 - Fixed on a circle. Does the Brouwer Fixed Point...Ch. 5.4 - Winding arrows. In each drawing below we have a...Ch. 5.4 - Prob. 10MSCh. 5.4 - Prob. 11MSCh. 5.4 - Home heating (H). Prove that there are two points...Ch. 5.4 - Prob. 13MSCh. 5.4 - Prob. 14MSCh. 5.4 - Prob. 15MSCh. 5.4 - Lining up (H). Suppose we have two line segments...Ch. 5.4 - A nice temp. Must there be two antipodal points on...Ch. 5.4 - Prob. 18MSCh. 5.4 - Diet drill. Suppose someone weighs 160 lbs. and...Ch. 5.4 - Speedy (S). You enter a tollway and are given a...Ch. 5.4 - The cut core. Suppose we have the red and blue...Ch. 5.4 - Fixed without boundary. Do you think that the...Ch. 5.4 - Take a hike (ExH). A hiker decides to climb up...Ch. 5.4 - Here we celebrate the power of algebra as a...Ch. 5.4 - Here we celebrate the power of algebra as a...Ch. 5.4 - Here we celebrate the power of algebra as a...Ch. 5.4 - Here we celebrate the power of algebra as a...Ch. 5.4 - Here we celebrate the power of algebra as a...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Solve each formula for the given letter . [2.3] What percent of 60 is 42? [2.4]
Elementary and Intermediate Algebra: Concepts and Applications (7th Edition)
The following set of data is from sample of n=5: a. Compute the mean, median, and mode. b. Compute the range, v...
Basic Business Statistics, Student Value Edition
At what points are the functions in Exercise continuous?
University Calculus: Early Transcendentals (4th Edition)
Fill in each blank so that the resulting statement is true. Any set of ordered pairs is called a/an ____.The se...
Algebra and Trigonometry (6th Edition)
In Exercises 5–12, identify whether the given value is a statistic or a parameter.
8. Triangle Fire Fatalities ...
Elementary Statistics (13th Edition)
Consider a group of 20 people. If everyone shakes hands with everyone else, how many handshakes take place?
A First Course in Probability (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 3. Which of the following mappings are linear transformations? Give a proof (directly using the definition of a linear transformation) or a counterexample in each case. [Recall that Pn(F) is the vector space of all real polynomials p(x) of degree at most n with values in F.] ·(2) = (3n+2) =) · (i) 0 : R³ → R² given by 0 y 3y z ax4 + bx² + c). (ii) : P2(F) → P₁(F) given by (p(x)) = p(x²) (so (ax² + bx + c) = ax4 þarrow_forward2. Let V be a vector space over F, and let U and W be subspaces of V. The sum of U and W, denoted by U + W, is the subset U + W = {u+w: u EU, w Є W}. Prove that U + W is a subspace of V.arrow_forward1. For the following subsets of vector spaces, state whether or not the indicated subset is a subspace. Justify your answers by giving a proof or a counter-example in each case. (i) The subset U = (ii) The subset V = {{ 2a+3b a+b b Є R³ : a, b Є R of the vector space R³. ER3 a+b+c=1 1}. of the vector space R³. = {() = (iii) The set D of matrices of determinant 0, in the vector space M2×2 (R) of all real 2×2 matrices. (iv) The set G of all polynomials p(x) with p(1) = p(0), in the vector space P3 of polynomials of degree at most 3 with coefficients in R. (v) The set Z of all sequences which are eventually zero, Z = {v = (vo, v1, v2,...) E F∞ there is n such that v; = 0 for all i ≥ n}, in the vector space F∞ of infinite sequences v = (vo, V1, V2, ...) with v¿ Є F (F any field).arrow_forward
- 4. For each of the following subspaces, find a basis, and state the dimension. (i) The subspace U = a 2b {(22) a+3b : a,bЄR of R³. (ii) The subspace W = x א > א (@ 3 ע 1 C4x + y + z = 0 and y − iz + w = 0 of C4.arrow_forward5. Given a subset {V1, V2, V3} of a vector space V over the field F, where F is a field with 1+1 ±0, show that {V1, V2, V3} is linearly independent if and only if {v1+V2, V2 + V3, V1 +V3} is linearly independent. [Note: V is an arbitrary vector space, not necessarily R" or Fn, so you cannot use the method of writing the vectors as the rows of a matrix.]arrow_forwardFind the flux F(x, y, z) = xi + 2yj +4zk, S is the cube with vertices (1, 1, 1), (-1, -1, -1)arrow_forward
- How does probability help businesses make informed decisions under uncertainty? Provide an example of how businesses use probability in marketing to predict customer behavior. Why is probability considered essential in financial decision-making, particularly in portfolio management? Discuss how the use of probability in inventory management can improve customer satisfaction. Compare the role of probability in marketing and financial decision-making. How do the applications differ in their objectives?arrow_forwardThe general solution of the linear system X' = AX is given. -6 ^ - (-3 %). A -5 4 -t ()()()] x(t) = c₁ 1 -t e + te + 1 e (a) In this case discuss the nature of the solutions in a neighborhood of (0, 0). All solutions spiral toward (0, 0). O All solutions become unbounded and y = x serves as the asymptote. O All solutions approach (0, 0) from the direction specified by y = x. If X(0) = X lies on the line x = 0, then X(t) approaches (0, 0) along this line. Otherwise x(t) approaches (0, 0) from the direction determined by y = x. If X(0) = X lies on the line y = x, then X(t) approaches (0, 0) along this line. Otherwise x(t) approaches (0, 0) from the direction determined by x = 0. (b) With the aid of a calculator or a CAS graph the solution that satisfies X(0) = (1, 1). 1.5 y -1.5 -1.0 -0.5 (1, 1) 1.0 0.5 -0.5 -1.0 -1.5 y 1.5 1.0 0.5 y 1.5 (1, 1) 1.0 0.5 X 0.5 1.0 1.5 -1.5 -1.0 -0,5 -0.5 -1.0 -1.5 y 1.5 EX 0.5 1.0 1.5 1.0 (1, 1) 0.5 X -1.5 -1.0 -0.5 -1.5 -1.0 -0.5 0.5 1.0 1.5 -0.5 -0.5…arrow_forward03: Let V = H(n), n≤ R, a(u,v) = (f, v) a(u,v) = Vu. Vv dx, and (f,v) = (a) Show that the finite element solution un unique. (b) Prove that || ≤ch ||||2 الكاملا (c) Given the triangulation of figure, determine the basis function and compute the integrals: So 4 dx, Sox where a (u,v) >, & ill 2 fvdx, v .V, dx. (0,1) V. V dx., SV. Vz dx. (0,0) (1,0)arrow_forward
- The general solution of the linear system X' = AX is given. A = = (³ -2). x(t) = c₁ c₁(1) et. et + c₂ e-t 3 3 (a) In this case discuss the nature of the solution in a neighborhood of (0, 0). O All solutions become unbounded and y = 3x serves as the asymptote. O All solutions become unbounded and y = x serves as the asymptote. If X(0) = X lies on the line y = x, then x(t) approaches (0, 0) along this line. Otherwise X(t) becomes unbounded and y = 3x serves as an asymptote. If X(0) = X lies on the line y = 3x, then x(t) approaches (0, 0) along this line. Otherwise x(t) becomes unbounded and y = x serves as an asymptote. O All solutions spiral toward (0, 0). (b) With the aid of a calculator or a CAS, graph the solution that satisfies X(0) = (1, 1). 2 1 (1, 1) x -2 -1 1 2 4 -2 2 1 (1, 1) 4 2 -2 (1, 1) 2 x 4 -4 i 2 (1, 1) 1 x 1 2 2 1 1 2 xarrow_forwardB-Solve the D.E of the following: 1- y+3y+2fy dt = f(t) for y(0)-1 if f(t) is the function whose graph is shown below 2- y" +4y = u(t) for y(0)-y'(0)-0 3- y"+4y+13y=e-2t sin3t 1 2 for y(0)-1 and y'(0)=-2arrow_forwardNo Chatgpt please Chatgpt means downvotearrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Basic Reflection Trigonometric Identity; Author: Anil kumar;https://www.youtube.com/watch?v=y-EGUD49fmw;License: Standard YouTube License, CC-BY