
(a) Write an expression for a Riemann sum of a function f. Explain the meaning of the notation that you use.
(b) If f(x) ≥ 0, what is the geometric interpretation of a Riemann sum? Illustrate with a diagram.
(c) If f(x) takes on both positive and negative values, what is the geometric interpretation of a Riemann sum? Illustrate with a diagram.
(a)
To find: The expression for a Riemann sum of a function
Answer to Problem 1CC
The expression for a Riemann sum of a function f is
Explanation of Solution
The Riemann sum of a function f is the method to find the total area underneath a curve.
The area under the curve dividedas n number of approximating rectangles. Hence the Riemann sum of a function f is the sum of the area of the all individual rectangles.
Here,
Thus, the expression for a Riemann sum of a function f is
b)
To define: The geometric interpretation of a Riemann sum with diagram.
Explanation of Solution
Given information:
Consider the condition for the function
The function
Sketch the curve
Show the curve as in Figure 1.
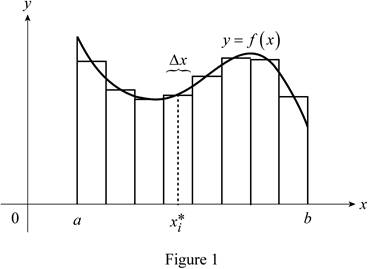
Refer to Figure 1
The function
Thus, the geometric interpretation of a Riemann sum of
c)
To define: The geometric interpretation of a Riemann sum, if the function
Explanation of Solution
Given information:
The function
The function
Sketch the curve
Show the curve as in Figure 2.
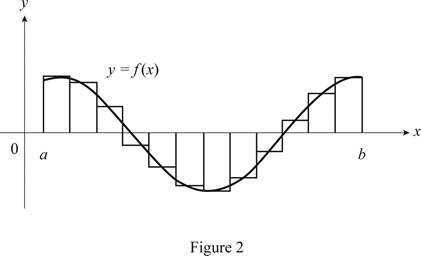
Refer figure 2,
The Riemann sum is the difference of areas of approximating rectangles above and below the x-axis
Therefore, the geometric interpretation of a Riemann sum is defined, if
Want to see more full solutions like this?
Chapter 5 Solutions
Calculus, Early Transcendentals
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
Elementary Statistics: Picturing the World (7th Edition)
Basic College Mathematics
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Introductory Statistics
Mathematics for the Trades: A Guided Approach (11th Edition) (What's New in Trade Math)
- Find the indefinite integral by making a change of variables. (Remember the constant of integration.) √(x+4) 4)√6-x dxarrow_forwarda -> f(x) = f(x) = [x] show that whether f is continuous function or not(by using theorem) Muslim_mathsarrow_forwardUse Green's Theorem to evaluate F. dr, where F = (√+4y, 2x + √√) and C consists of the arc of the curve y = 4x - x² from (0,0) to (4,0) and the line segment from (4,0) to (0,0).arrow_forward
- Evaluate F. dr where F(x, y, z) = (2yz cos(xyz), 2xzcos(xyz), 2xy cos(xyz)) and C is the line π 1 1 segment starting at the point (8, ' and ending at the point (3, 2 3'6arrow_forwardCan you help me find the result of an integral + a 炉[メをメ +炉なarrow_forward2 a Can you help me find the result of an integral a 아 x² dxarrow_forward
- Please help me with this question as I want to know how can I perform the partial fraction decompostion on this alebgric equation to find the time-domain of y(t)arrow_forwardPlease help me with this question as I want to know how can I perform the partial fraction on this alebgric equation to find the time-domain of y(t)arrow_forwardEvaluate F³ - dr where ♬ = (4z, -4y, x), and C' is given by (t) = (sin(t), t, cos(t)), 0≤t≤ñ .arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

 Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning  College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning



