Bundle: Principles of Physics: A Calculus-Based Text, 5th + WebAssign Printed Access Card for Serway/Jewett's Principles of Physics: A Calculus-Based Text, 5th Edition, Multi-Term
5th Edition
ISBN: 9781133422013
Author: Raymond A. Serway; John W. Jewett
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 3, Problem 21P
A playground is on the flat roof of a city school, 6.00 m above the street below (Fig. P3.21). The vertical wall of the building is h = 7.00 m high, forming a 1-m-high railing around the playground. A ball has fallen to the street below, and a passerby returns it by launching it at an angle of θ = 53.0° above the horizontal at a point d = 24.0 m from the base of the building wall. The ball takes 2.20 s to reach a point vertically above the wall. (a) Find the speed at which the ball was launched. (b) Find the vertical distance by which the ball clears the wall. (c) Find the horizontal distance from the wall to the point on the roof where the ball lands.
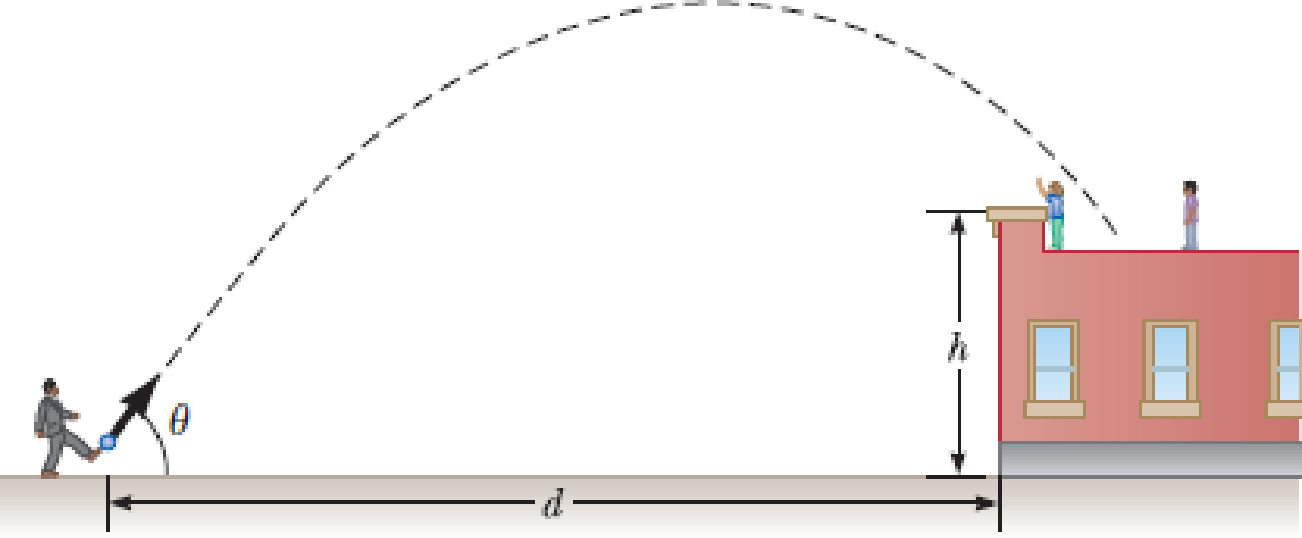
Figure P3.21
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Please Asap
A playground is on the flat roof of a city school, hb = 4.60 m above the street below. The vertical wall of the building is h = 6.10 m high, to form a 1.5-m-high railing around the playground. A ball has fallen to the street below, and a passerby returns it by launching it at an angle of ? = 53.0° above the horizontal at a point d = 24.0 m from the base of the building wall. The ball takes 2.20 s to reach a point vertically above the wall.
(a) Find the speed at which the ball was launched.
(b) Find the vertical distance by which the ball clears the wall.
(c) Find the horizontal distance from the wall to the point on the roof where the ball lands.
A playground is on the flat roof of a city school, hb = 6.40 m above the street below (see figure). The vertical wall of the building is h = 7.70 m high, to form a 1.3-m-high railing around the playground. A ball has fallen to the street below, and a passerby returns it by launching it at an angle of ? = 53.0° above the horizontal at a point d = 24.0 m from the base of the building wall. The ball takes 2.20 s to reach a point vertically above the wall.
(a) Find the speed at which the ball was launched. m/s = (b) Find the vertical distance by which the ball clears the wall. m =(c) Find the horizontal distance from the wall to the point on the roof where the ball lands. m =
Chapter 3 Solutions
Bundle: Principles of Physics: A Calculus-Based Text, 5th + WebAssign Printed Access Card for Serway/Jewett's Principles of Physics: A Calculus-Based Text, 5th Edition, Multi-Term
Ch. 3.1 - Consider the following controls in an automobile...Ch. 3.3 - (i) As a projectile thrown upward moves in its...Ch. 3.3 - Rank the launch angles for the five paths in...Ch. 3.4 - Which of the following correctly describes the...Ch. 3.5 - A particle moves along a path, and its speed...Ch. 3 - In which of the following situations is the moving...Ch. 3 - A rubber stopper on the end of a string is swung...Ch. 3 - Figure OQ3.3 shows a birds-eye view of a car going...Ch. 3 - Entering his dorm room, a student tosses his book...Ch. 3 - Does a car moving around a circular track with...
Ch. 3 - An astronaut hits a golf ball on the Moon. Which...Ch. 3 - A projectile is launched on the Earth with a...Ch. 3 - A baseball is thrown from the outfield toward the...Ch. 3 - A student throws a heavy red ball horizontally...Ch. 3 - A sailor drops a wrench from the top of a...Ch. 3 - A set of keys on the end of a string is swung...Ch. 3 - Prob. 12OQCh. 3 - Prob. 1CQCh. 3 - Prob. 2CQCh. 3 - Prob. 3CQCh. 3 - Prob. 4CQCh. 3 - Prob. 5CQCh. 3 - Prob. 6CQCh. 3 - A projectile is launched at some angle to the...Ch. 3 - A motorist drives south at 20.0 m/s for 3.00 min,...Ch. 3 - Prob. 2PCh. 3 - A particle initially located at the origin has an...Ch. 3 - It is not possible to see very small objects, such...Ch. 3 - A fish swimming in a horizontal plane has velocity...Ch. 3 - At t = 0, a particle moving in the xy plane with...Ch. 3 - Mayan kings and many school sports teams are named...Ch. 3 - The small archerfish (length 20 to 25 cm) lives in...Ch. 3 - Prob. 9PCh. 3 - Prob. 10PCh. 3 - Prob. 11PCh. 3 - Prob. 12PCh. 3 - Prob. 13PCh. 3 - Prob. 14PCh. 3 - Prob. 15PCh. 3 - A firefighter, a distance d from a burning...Ch. 3 - A soccer player kicks a rock horizontally off a...Ch. 3 - Prob. 18PCh. 3 - A student stands at the edge of a cliff and throws...Ch. 3 - Prob. 20PCh. 3 - A playground is on the flat roof of a city school,...Ch. 3 - Prob. 22PCh. 3 - Prob. 23PCh. 3 - Prob. 24PCh. 3 - As their booster rockets separate, Space Shuttle...Ch. 3 - Prob. 26PCh. 3 - The astronaut orbiting the Earth in Figure P3.27...Ch. 3 - Prob. 28PCh. 3 - Prob. 29PCh. 3 - A point on a rotating turntable 20.0 cm from the...Ch. 3 - Figure P3.31 represents the total acceleration of...Ch. 3 - Prob. 32PCh. 3 - Prob. 33PCh. 3 - Prob. 34PCh. 3 - Prob. 35PCh. 3 - Prob. 36PCh. 3 - Prob. 37PCh. 3 - Prob. 38PCh. 3 - Prob. 39PCh. 3 - Prob. 40PCh. 3 - A certain light truck can go around an unbanked...Ch. 3 - A landscape architect is planning an artificial...Ch. 3 - Why is the following situation impassible? A...Ch. 3 - An astronaut on the surface of the Moon fires a...Ch. 3 - The Vomit Comet. In microgravity astronaut...Ch. 3 - A projectile is fired up an incline (incline angle...Ch. 3 - A basketball player is standing on the floor 10.0...Ch. 3 - A truck loaded with cannonball watermelons stops...Ch. 3 - A ball on the end of a string is whirled around in...Ch. 3 - An outfielder throws a baseball to his catcher in...Ch. 3 - Prob. 51PCh. 3 - A skier leaves the ramp of a ski jump with a...Ch. 3 - A World War II bomber flies horizontally over...Ch. 3 - A ball is thrown with an initial speed vi at an...Ch. 3 - Prob. 55PCh. 3 - A person standing at the top of a hemispherical...Ch. 3 - An aging coyote cannot run fast enough to catch a...Ch. 3 - Prob. 58PCh. 3 - The water in a river flows uniformly at a constant...Ch. 3 - Prob. 61P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A hiker walks from (x1, y1) = (4.00 km. 3.00 km) to (x2, y2) = (3.00 km, 6.00 km), (a) What distance has the traveled? (b) The hiker desires to return to his starting point. In what direction should he go? (Give the angle with respect to due cast.) (See Sections 3.2 and 3.3.)arrow_forwardOlympus Mons on Mars is the largest volcano in the solar system, at a height of 25 km and with a radius of 312 km. If you are standing on the summit, with what Initial velocity would you have to fire a projectile from a cannon horizontally to clear the volcano and land on the surface of Mars? Note that Mars has an acceleration of gravity of 3.7m/s2 .arrow_forwardA playground is on the flat roof of a city school, hb = 5.70 m above the street. The vertical wall of the building is h = 7.10 m high, to form a 1.4-m-high railing around the playground. A ball has fallen to the street, and a passerby returns it by launching it at an angle of Ø= 53.0° above the horizontal at a point d = 24.0m from the base of the building wall. The ball takes 2.20 s to reach a point vertically above the wall. (a) Find the speed at which the ball was launched. (b) Find the vertical distance by which the ball clears the wall. (c) Find the horizontal distance from the wall to the point on the roof where the ball lands.arrow_forward
- A playground is on the flat roof of a city school, hb = 6.70 m above the street below (see figure). The vertical wall of the building is h = 7.90 m high, to form a 1.2-m-high railing around the playground. A ball has fallen to the street below, and a passerby returns it by launching it at an angle of ? = 53.0° above the horizontal at a point d = 24.0 m from the base of the building wall. The ball takes 2.20 s to reach a point vertically above the wall. Question: (a) Find the speed at which the ball was launched.arrow_forwardA playground is on the flat roof of a city school, hb = 6.70 m above the street below (see figure). The vertical wall of the building is h = 7.90 m high, to form a 1.2-m-high railing around the playground. A ball has fallen to the street below, and a passerby returns it by launching it at an angle of ? = 53.0° above the horizontal at a point d = 24.0 m from the base of the building wall. The ball takes 2.20 s to reach a point vertically above the wall. A man on the ground kicking a ball to children on a flat rooftop is shown. The distance between the man and the building is labeled d. The height of the left wall of the building is labeled h. The motion of the ball is depicted as a parabola originating from the man on the ground and ending at the rooftop. The vector of the initial motion of the ball makes an angle ? with the horizontal. (b) Find the vertical distance by which the ball clears the wall. m(c) Find the horizontal distance from the wall to the point on the roof where the…arrow_forwardA playground is on the flat roof of a city school, hb = 5.00 m above the street below (see figure). The vertical wall of the building is h = 6.20 m high, to form a 1.2-m-high railing around the playground. A ball has fallen to the street below, and a passerby returns it by launching it at an angle of θ = 53.0° above the horizontal at a point d = 24.0 m from the base of the building wall. The ball takes 2.20 s to reach a point vertically above the wall. A man on the ground kicking a ball to children on a flat rooftop is shown. The distance between the man and the building is labeled d. The height of the left wall of the building is labeled h. The motion of the ball is depicted as a parabola originating from the man on the ground and ending at the rooftop. The vector of the initial motion of the ball makes an angle θ with the horizontal. (a) Find the speed at which the ball was launched. m/s(b) Find the vertical distance by which the ball clears the wall. m(c) Find the horizontal…arrow_forward
- A playground is on the flat roof of a city school, 6.00m above the street below. The vertical wall of the building is h=7.00m high, forming a 1-m-high railing around the playground. A ball has fallen to the street below, and a passerby returns it by launching it at an angle of ɵ=53.0o above the horizontal at a point d=24.0 m from the base of the building wall. The ball takes 2.20s to reach a point vertically above the wall. Find the vertical distance by which the ball clears the wall. show the complete solution.arrow_forwardA playground is on the flat roof of a city school, 6.00 m above the street below (Fig. P3.34). The vertical wall of the building is h = 7.00 m high, to form a 1-m-high railing around the playground. A ball has fallen to the street below, and a passerby returns it by launching it at an angle of θ = 53.0° above the horizontal at a point d = 24.0 m from the base of the building wall. The ball takes 2.20 s to reach a point vertically above the wall. (a) Find the speed at which the ball was launched. (b) Find the vertical distance by which the ball clears the wall. (c) Find the horizontal distance from the wall to the point on the roof where the ball lands.arrow_forwardA playground is on the flat roof of a city school, hb = 5.10 m above the street below (see figure). The vertical wall of the building is h = 6.50 m high, to form a 1.4-m-high railing around the playground. A ball has fallen to the street below, and a passerby returns it by launching it at an angle of θ = 53.0° above the horizontal at a point d = 24.0 m from the base of the building wall. The ball takes 2.20 s to reach a point vertically above the wall. (a) Find the speed at which the ball was launched.m/s(b) Find the vertical distance by which the ball clears the wall.m(c) Find the horizontal distance from the wall to the point on the roof where the ball lands.marrow_forward
- A playground is on the flat roof of a city school, 6.1 m above the street below (see figure). The vertical wall of the building is h = 7.60 m high, forming a 1.5-m-high railing around the playground. A ball has fallen to the street below, and a passerby returns it by launching it at an angle of e = 53.0° above the horizontal at a point d = 24.0 m from the base of the building wall. The ball takes 2.20 s to reach a point vertically above the wall. (a) Find the speed at which the ball was launched. (Give your answer to two decimal places to reduce rounding errors in later parts.) m/s (b) Find the vertical distance by which the ball clears the wall. (c) Find the horizontal distance from the wall to the point on the roof where the ball lands. marrow_forwardA playground is on the flat roof of a city school, 6.00 m abovethe street below (Fig. P3.19). The vertical wall of the buildingis h = 7.00 m high, to form a 1-m-high railing around the playground.A ball has fallen to the street below, and a passerbyreturns it by launching it at an angle of θ = 53.0° above thehorizontal at a point d = 24.0 m from the base of the buildingwall. The ball takes 2.20 s to reach a point vertically abovethe wall. (a) Find the speed at which the ball was launched.(b) Find the vertical distance by which the ball clears the wall.(c) Find the horizontal distance from the wall to the point onthe roof where the ball lands.arrow_forwardA playground is on the flat roof of a city school, hb = 4.80 m above the street below (see figure). The vertical wall of the building is h = 6.10 m high, to form a 1.3-m-high railing around the playground. A ball has fallen to the street below, and a passerby returns it by launching it at an angle of θ = 53.0° above the horizontal at a point d = 24.0 m from the base of the building wall. The ball takes 2.20 s to reach a point vertically above the wall. (a) Find the speed at which the ball was launched. m/s(b) Find the vertical distance by which the ball clears the wall. m(c) Find the horizontal distance from the wall to the point on the roof where the ball lands. marrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
University Physics Volume 1
Physics
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:OpenStax - Rice University
College Physics
Physics
ISBN:9781285737027
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
Kinematics Part 3: Projectile Motion; Author: Professor Dave explains;https://www.youtube.com/watch?v=aY8z2qO44WA;License: Standard YouTube License, CC-BY