Concept explainers
Videos
For the waveforms in Fig. 26.32, determine whether the following will be present in the Fourier series representation:
a. dc term
b. cosine terms
c. sine terms
d. even-ordered harmonics
e. odd-ordered harmonics
(a)
Whether dc term, cosine terms, sine terms, even ordered harmonics and odd ordered harmonics will be present in the given Fourier Series representation or not.
Answer to Problem 1P
The D.C. term is not present in the waveform, cosine terms are not present in the waveform, sine terms are present in the waveform, even ordered harmonics are not present in the waveform and odd ordered harmonics are present in the waveform.
Explanation of Solution
Calculation:
The waveform for Fourier series representation is drawn as shown in Figure 1.
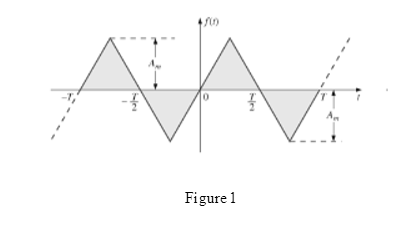
Case 1:
D.C. value is the average value of the waveform. And as the area above the horizontal axis and below the horizontal axis is equal, so the value of area and the average is zero for the waveform.
Therefore, D.C. term is not present in the waveform.
Case 2:
If waveform is symmetric about vertical axis, it has an even symmetry. And for an even symmetry, the wave Fourier series contains D.C. and cosine term.
As waveform is not symmetric about the vertical axis, it means cosine terms are not present in the waveform.
Case 3:
If waveform is symmetric about origin it has odd symmetry. And for odd symmetry wave Fourier series contain D.C. and sine term.
As waveform is symmetric about origin, it means sine terms are present in the waveform.
Case 4:
Cosine term is even function and sine terms are odd function.
As waveform does not contain cosine term, therefore, even ordered harmonics are not present in the waveform.
Case 5:
Cosine term is even function and sine terms are odd function.
As the waveform contains sine term, therefore, odd ordered harmonics are present in the waveform.
Conclusion:
Thus, D.C. term is not present in the waveform, cosine terms are not present in the waveform, sine terms are present in the waveform, even ordered harmonics are not present in the waveform and odd ordered harmonics are present in the waveform.
(b)
Whether dc term, cosine terms, sine terms, even ordered harmonics and odd ordered harmonics will be present in the given Fourier Series representation or not.
Answer to Problem 1P
The D.C. term is present in the waveform, cosine terms are not present in the waveform, sine terms are not present in the waveform, even ordered harmonics are not present in the waveform and odd ordered harmonics are not present in the waveform.
Explanation of Solution
Calculation:
The waveform for Fourier series representation is drawn as shown in Figure 2.
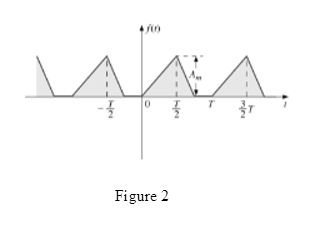
Case 1:
D.C. value is the average value of the waveform. And as area above the horizontal axis and below the horizontal axis is not equal so value of area and average is not zero for the waveform.
Therefore D.C. term is present in the waveform.
Case 2:
If waveform is symmetric about vertical axis it has even symmetry. And for even symmetry wave Fourier series contain D.C. and cosine term.
As waveform is not symmetric about vertical axis it means cosine terms are not present in the waveform.
Case 3:
If waveform is symmetric about origin it has odd symmetry. And for odd symmetry wave Fourier series contain D.C. and sine term.
As waveform is not symmetric about origin it means sine terms are not present in the waveform.
Case 4:
Cosine term is even function and sine terms are odd function.
As waveform does not contain cosine term therefore even ordered harmonics are not present in the waveform.
Case 5:
Cosine term is even function and sine terms are odd function.
As waveform does not contains sine term therefore odd ordered harmonics are not present in the waveform.
Conclusion:
Thus, D.C. term is present in the waveform, cosine terms are not present in the waveform, sine terms are not present in the waveform, even ordered harmonics are not present in the waveform and odd ordered harmonics are not present in the waveform.
(c)
Whether dc term, cosine terms, sine terms, even ordered harmonics and odd ordered harmonics will be present in the given Fourier Series representation or not.
Answer to Problem 1P
The D.C. term is present in the waveform, cosine terms are present in the waveform, sine terms are not present in the waveform, even ordered harmonics are present in the waveform and odd ordered harmonics are not present in the waveform.
Explanation of Solution
Calculation:
The waveform for Fourier series representation is drawn as shown in Figure 3.
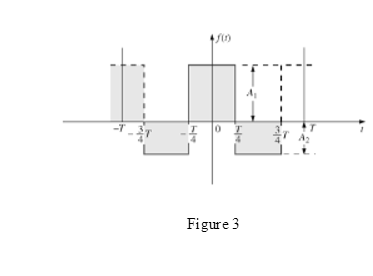
Case 1:
D.C. value is the average value of the waveform. And as area above the horizontal axis and below the horizontal axis is not equal so value of area and average is not zero for the waveform.
Therefore D.C. term is present in the waveform.
Case 2:
If waveform is symmetric about vertical axis it has even symmetry. And for even symmetry wave Fourier series contain D.C. and cosine term.
As waveform is symmetric about vertical axis it means cosine terms are present in the waveform.
Case 3:
If waveform is symmetric about origin it has odd symmetry. And for odd symmetry wave Fourier series contain D.C. and sine term.
As waveform is not symmetric about origin it means sine terms are not present in the waveform.
Case 4:
Cosine term is even function and sine terms are odd function.
As waveform contain cosine term therefore even ordered harmonics are present in the waveform.
Case 5:
Cosine term is even function and sine terms are odd function.
As waveform does not contains sine term therefore odd ordered harmonics are not present in the waveform.
Conclusion:
Thus, D.C. term is present in the waveform, cosine terms are present in the waveform, sine terms are not present in the waveform, even ordered harmonics are present in the waveform and odd ordered harmonics are not present in the waveform.
(d)
Whether dc term, cosine terms, sine terms, even ordered harmonics and odd ordered harmonics will be present in the given Fourier Series representation or not.
Answer to Problem 1P
The D.C. term is present in the waveform, cosine terms are not present in the waveform, sine terms are present in the waveform, even ordered harmonics are not present in the waveform and odd ordered harmonics are present in the waveform.
Explanation of Solution
Calculation:
The waveform for Fourier series representation is drawn as shown in Figure 4.
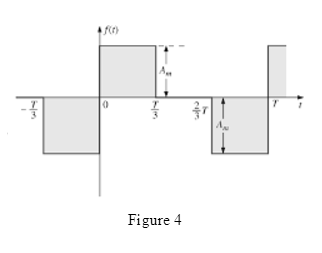
Case 1:
D.C. value is the average value of the waveform. And as area above the horizontal axis and below the horizontal axis is equal so value of area and average is zero for the waveform.
Therefore D.C. term is present in the waveform.
Case 2:
If waveform is symmetric about vertical axis it has even symmetry. And for even symmetry wave Fourier series contain D.C. and cosine term.
As waveform is not symmetric about vertical axis it means cosine terms are not present in the waveform.
Case 3:
If waveform is symmetric about origin it has odd symmetry. And for odd symmetry wave Fourier series contain D.C. and sine term.
As waveform is symmetric about origin it means sine terms are present in the waveform.
Case 4:
Cosine term is even function and sine terms are odd function.
As waveform does not contain cosine term therefore even ordered harmonics are not present in the waveform.
Case 5:
Cosine term is even function and sine terms are odd function.
As waveform contains sine term therefore odd ordered harmonics are present in the waveform.
Conclusion:
Thus, D.C. term is present in the waveform, cosine terms are not present in the waveform, sine terms are present in the waveform, even ordered harmonics are not present in the waveform and odd ordered harmonics are present in the waveform.
Want to see more full solutions like this?
Chapter 26 Solutions
Introductory Circuit Analysis (13th Edition)
- Don't use ai to answer I will report you answerarrow_forwardDon't use ai to answer I will report you answerarrow_forwardI have a problem getting the time domain of system S, can you plz show me from where I should start until find the time domain equation of the system to transfer it to z-domain.arrow_forward
- Q3arrow_forwardGiven the logic function F(A,B,C,D) = Σm(1,2,3,4,9,10,11,12) (i) Write the truth table of the logic function. (ii) Use the Karnaugh-map method to find the simplest sum-of-products (SOP) expression of function F. (iii) Implement the minimized function with NAND gates only. (iv) Show that the Boolean function F can be constructed using exclusive-OR gates (v) Express the same logic function in a product-of-sums (POS) form. (vi) Simplify your function in product-of-sums (POS). (vii) Use a decoder with external AND gates only to implement F in its product-of- sums (POS) form (assume AND gates with any number of inputs are available). Note: You can use NAND gates with any number of inputs you may need. Assume, as well, that the input variables are available in both true and complemented form.arrow_forwardProblem A medical research facility is developing a proton accelerator for cancer treatment using proton therapy. The accelerator is designed to generate a beam of protons that precisely targets and destroys cancerous cells while minimizing damage to surrounding healthy tissue. However, there is an issue with the beam trajectory, which deviates from the intended direction when subjected to electric and magnetic fields. A team of engineers has been assigned to diagnose and resolve this issue. -The accelerator generates a beam of 10" protons with an initial velocity of v = 3 × 10° m/s in the y-axis direction. -An electric field of E = 200 kV/m is applied in the negative z-axis using a set of electrodes. -A magnetic field of B = 0.1T is applied along the z-axis using a solenoid to redirect the protons. - However, the beam does not align with the expected trajectory, indicating an error in field configuration or an unaccounted force acting on the protons. Answer the following questions 1.…arrow_forward
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,