Calculus & Its Applications
12th Edition
ISBN: 9780137590810
Author: Larry J. Goldstein, David C. Lay, David I. Schneider, Nakhle H. Asmar, William Edward Tavernetti
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 2.5, Problem 1CYU
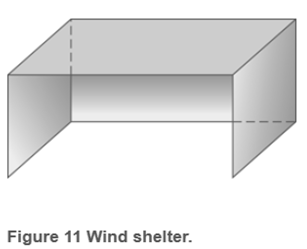
Volume A canvas wind shelter for the beach has a back, two square sides, and a top (Fig.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
An object of mass 4 kg is given an initial downward velocity of 60 m/sec and then allowed to fall under the influence of gravity. Assume that the force in newtons due to air resistance is - 8v, where v is the velocity
of the object in m/sec. Determine the equation of motion of the object. If the object is initially 500 m above the ground, determine when the object will strike the ground. Assume that the acceleration due to gravity
is 9.81 m/sec² and let x(t) represent the distance the object has fallen in t seconds.
Determine the equation of motion of the object.
x(t) =
(Use integers or decimals for any numbers in the expression. Round to two decimal places as needed.)
Early Monday morning, the temperature in the lecture hall has fallen to 40°F, the same as the temperature outside. At 7:00 A.M., the janitor turns on the furnace with the thermostat set at 72°F. The time constant
for the building is = 3 hr and that for the building along with its heating system is
1
K
A.M.? When will the temperature inside the hall reach 71°F?
1
=
1
hr. Assuming that the outside temperature remains constant, what will be the temperature inside the lecture hall at 8:30
2
At 8:30 A.M., the temperature inside the lecture hall will be about
(Round to the nearest tenth as needed.)
1°F.
Find the maximum volume of a rectangular box whose surface area is 1500 cm² and whose total edge
length is 200 cm.
cm³
Chapter 2 Solutions
Calculus & Its Applications
Ch. 2.1 - Does the slope of the curve in Fig. 17 increases...Ch. 2.1 - At which labelled point on the graph in Fig. 18 is...Ch. 2.1 - Exercises 1-4 refer to graphs (a)-(f) in Fig.19...Ch. 2.1 - Exercises 1-4 refer to graphs (a)-(f) in Fig.19...Ch. 2.1 - Exercises 1-4 refer to graphs (a)-(f) in Fig.19...Ch. 2.1 - Exercises 1-4 refer to graphs (a)-(f) in Fig.19...Ch. 2.1 - Describe each of the following graphs. Your...Ch. 2.1 - Describe each of the following graphs. Your...Ch. 2.1 - Describe each of the following graphs. Your...Ch. 2.1 - Describe each of the following graphs. Your...
Ch. 2.1 - Describe each of the following graphs. Your...Ch. 2.1 - Prob. 10ECh. 2.1 - Describe each of the following graphs. Your...Ch. 2.1 - Prob. 12ECh. 2.1 - Describe the way the slope changes as you move...Ch. 2.1 - Prob. 14ECh. 2.1 - Describe the way the slope changes on the graph in...Ch. 2.1 - Prob. 16ECh. 2.1 - Exercise 17 and 18 refer to the graph in Fig 20....Ch. 2.1 - Exercise 17 and 18 refer to the graph in Fig 20....Ch. 2.1 - Prob. 19ECh. 2.1 - In Exercises 19-22, draw the graph of a function...Ch. 2.1 - In Exercises 19-22, draw the graph of a function...Ch. 2.1 - Prob. 22ECh. 2.1 - Prob. 23ECh. 2.1 - Prob. 24ECh. 2.1 - A Patients Temperature At noon, a childs...Ch. 2.1 - Prob. 26ECh. 2.1 - Blood Flow through the Brain One method of...Ch. 2.1 - Pollution Suppose that some organic waste products...Ch. 2.1 - Prob. 29ECh. 2.1 - Prob. 30ECh. 2.1 - Prob. 31ECh. 2.1 - Let P(t) be the population of a bacteria culture...Ch. 2.1 - In Exercises 3336, sketch the graph of a function...Ch. 2.1 - In Exercises 3336, sketch the graph of a function...Ch. 2.1 - In Exercises 3336, sketch the graph of a function...Ch. 2.1 - In Exercises 3336, sketch the graph of a function...Ch. 2.1 - Consider a smooth curve with no undefined points....Ch. 2.1 - If the function f(x) has a relative minimum at x=a...Ch. 2.1 - Technology Exercises Graph the function...Ch. 2.1 - Prob. 40ECh. 2.1 - Technology Exercises Simultaneously graph the...Ch. 2.2 - Make a good sketch of the function f(x) near the...Ch. 2.2 - The graph of f(x)=x3 is shown in Fig. 15. Is the...Ch. 2.2 - The graph of y=f(x) is shown in Fig. 16. Explain...Ch. 2.2 - Exercises 14 refer to the functions whose graphs...Ch. 2.2 - Exercises 14 refer to the functions whose graphs...Ch. 2.2 - Exercises 14 refer to the functions whose graphs...Ch. 2.2 - Exercises 14 refer to the functions whose graphs...Ch. 2.2 - Which one of the graph in Fig. 18 could represent...Ch. 2.2 - Which one of the graphs in Fig. 18 could represent...Ch. 2.2 - In Exercises 712, sketch the graph of a function...Ch. 2.2 - In Exercises 712, sketch the graph of a function...Ch. 2.2 - In Exercises 712, sketch the graph of a function...Ch. 2.2 - In Exercises 712, sketch the graph of a function...Ch. 2.2 - In Exercises 712, sketch the graph of a function...Ch. 2.2 - In Exercises 712, sketch the graph of a function...Ch. 2.2 - In Exercises 1318, use the given information to...Ch. 2.2 - In Exercises 1318, use the given information to...Ch. 2.2 - In Exercises 1318, use the given information to...Ch. 2.2 - In Exercises 1318, use the given information to...Ch. 2.2 - In Exercises 1318, use the given information to...Ch. 2.2 - In Exercises 1318, use the given information to...Ch. 2.2 - Refer to the graph in Fig. 19. Fill in each box of...Ch. 2.2 - The first and second derivatives of the function...Ch. 2.2 - Suppose that Fig. 20 contains the graph of y=s(t),...Ch. 2.2 - Suppose that Fig. 20 contains the graph of y=v(t),...Ch. 2.2 - 23. Refer to figure 21, Looking at the graph f(x),...Ch. 2.2 - In figure 22, the t axis represent the time in...Ch. 2.2 - 25. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - 26. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - 27. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - 28. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - 29. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - 30. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - 31. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - Prob. 32ECh. 2.2 - 33. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - 34. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - 35. Exercises 2536 refer to Fig. 23, which...Ch. 2.2 - Prob. 36ECh. 2.2 - 37. Level of Water from Melting Snow Melting snow...Ch. 2.2 - 38. Changes in Temperature T(t) is the temperature...Ch. 2.2 - Prob. 39ECh. 2.2 - Prob. 40ECh. 2.2 - Prob. 41ECh. 2.2 - 42. Match each observation (a)(e) with a...Ch. 2.2 - Prob. 43ECh. 2.2 - Drug Diffusion in the Bloodstream After a drug is...Ch. 2.2 - Prob. 45ECh. 2.2 - Prob. 46ECh. 2.3 - Which of the curves in Fig.15 could possibly be...Ch. 2.3 - Which of the curves in Fig.16 could be the graph...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Prob. 14ECh. 2.3 - Prob. 15ECh. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Each of the graphs of the functions in Exercises...Ch. 2.3 - Prob. 24ECh. 2.3 - Sketch the following curves, indicating all...Ch. 2.3 - Sketch the following curves, indicating all...Ch. 2.3 - Sketch the following curves, indicating all...Ch. 2.3 - Sketch the following curves, indicating all...Ch. 2.3 - Sketch the following curves, indicating all...Ch. 2.3 - Sketch the following curves, indicating all...Ch. 2.3 - Prob. 31ECh. 2.3 - Prob. 32ECh. 2.3 - Prob. 33ECh. 2.3 - Let a,b,c,d be fixed numbers with a0, and let...Ch. 2.3 - The graph of each function in Exercises 35 40 has...Ch. 2.3 - Prob. 36ECh. 2.3 - The graph of each function in Exercises 35 40 has...Ch. 2.3 - The graph of each function in Exercises 35 40 has...Ch. 2.3 - The graph of each function in Exercises 35 40 has...Ch. 2.3 - The graph of each function in Exercises 35 40 has...Ch. 2.3 - In Exercises 41 and 42, determine which function...Ch. 2.3 - In Exercises 41 and 42, determine which function...Ch. 2.3 - Consider the graph of g(x) in Fig. 17. a. If g(x)...Ch. 2.3 - U. S. Population The population (in millions) of...Ch. 2.3 - Index-Fund Fees When a mutual fund company charges...Ch. 2.3 - Prob. 46ECh. 2.3 - Technology Exercises Draw the graph of...Ch. 2.3 - Technology Exercises Draw the graph of...Ch. 2.3 - Technology Exercises Draw the graph of...Ch. 2.3 - Technology Exercises Draw the graph of...Ch. 2.4 - Determine whether each of the following functions...Ch. 2.4 - Prob. 2CYUCh. 2.4 - Prob. 3CYUCh. 2.4 - Find the x intercepts of the given function....Ch. 2.4 - Prob. 2ECh. 2.4 - Find the x intercepts of the given function....Ch. 2.4 - Prob. 4ECh. 2.4 - Find the x intercepts of the given function....Ch. 2.4 - Find the x intercepts of the given function....Ch. 2.4 - Show that the function f(x)=13x32x2+5x has no...Ch. 2.4 - Prob. 8ECh. 2.4 - Sketch the graphs of the following functions....Ch. 2.4 - Sketch the graphs of the following functions....Ch. 2.4 - Sketch the graphs of the following functions....Ch. 2.4 - Sketch the graphs of the following functions....Ch. 2.4 - Sketch the graphs of the following functions....Ch. 2.4 - Prob. 14ECh. 2.4 - Sketch the graphs of the following functions....Ch. 2.4 - Prob. 16ECh. 2.4 - Sketch the graphs of the following functions....Ch. 2.4 - Prob. 18ECh. 2.4 - Sketch the graphs of the following functions....Ch. 2.4 - Sketch the graphs of the following functions....Ch. 2.4 - Prob. 21ECh. 2.4 - Prob. 22ECh. 2.4 - Sketch the graphs of the following functions for...Ch. 2.4 - Prob. 24ECh. 2.4 - Sketch the graphs of the following functions for...Ch. 2.4 - Prob. 26ECh. 2.4 - Sketch the graphs of the following functions for...Ch. 2.4 - Prob. 28ECh. 2.4 - Prob. 29ECh. 2.4 - Prob. 30ECh. 2.4 - Prob. 31ECh. 2.4 - Prob. 32ECh. 2.4 - Find the quadratic function f(x)=ax2+bx+c that...Ch. 2.4 - Prob. 34ECh. 2.4 - Prob. 35ECh. 2.4 - Prob. 36ECh. 2.4 - Prob. 37ECh. 2.4 - Technology Exercises Height of Tropical Grass The...Ch. 2.5 - Volume A canvas wind shelter for the beach has a...Ch. 2.5 - Prob. 2CYUCh. 2.5 - For what x does the function g(x)=10+40xx2 have...Ch. 2.5 - Find the maximum value of the function f(x)=12xx2,...Ch. 2.5 - Find the minimum value of f(t)=t36t2+40, t0 and...Ch. 2.5 - For what t does the function f(t)=t2-24t have its...Ch. 2.5 - Optimization with Constraint Find the maximum of...Ch. 2.5 - Optimization with Constraint Find two positive...Ch. 2.5 - Optimization with Constraint Find the minimum of...Ch. 2.5 - In Exercise 7, can there be a maximum for Q=x2+y2...Ch. 2.5 - Minimizing a Sum Find the positive values of x and...Ch. 2.5 - Maximizing a Product Find the positive values of...Ch. 2.5 - Area There are 320 available to fence in a...Ch. 2.5 - Volume Figure 12 (b) shows an open rectangular box...Ch. 2.5 - Volume Postal requirements specify that parcels...Ch. 2.5 - Perimeter Consider the problem of finding the...Ch. 2.5 - Cost A rectangular garden of area 75 square feet...Ch. 2.5 - Cost A closed rectangular box with a square base...Ch. 2.5 - Surface Area Find the dimensions of the closed...Ch. 2.5 - Volume A canvas wind shelter for the beach has a...Ch. 2.5 - Area A farmer has 1500 available to build an...Ch. 2.5 - Area Find the dimensions of the rectangular garden...Ch. 2.5 - Maximizing a Product Find two positive numbers,...Ch. 2.5 - Minimizing a Sum Find two positive numbers, xandy,...Ch. 2.5 - Area Figure 140 (a) shows a Norman window, which...Ch. 2.5 - Surface Area A large soup can is to be designed so...Ch. 2.5 - In Example 3 we can solve the constraint equation...Ch. 2.5 - Cost A ship uses 5x2 dollars of fuel per hour when...Ch. 2.5 - Cost A cable is to be installed from one corner,...Ch. 2.5 - Area A rectangular page is to contain 50 square...Ch. 2.5 - Distance Find the point on the graph of y=x that...Ch. 2.5 - Prob. 30ECh. 2.5 - Distance Find the point on the line y=2x+5 that is...Ch. 2.5 - Technology Exercise Inscribed Rectangle of Maximum...Ch. 2.6 - In the inventory problem of Example 2, suppose...Ch. 2.6 - In the inventory problem Example 2, Suppose that...Ch. 2.6 - Inventory Problem Figure 6 shows the inventory...Ch. 2.6 - Refer to Fig. 6. Suppose that The ordering cost...Ch. 2.6 - Inventory Control A pharmacist wants to establish...Ch. 2.6 - Inventory Control A furniture store expects to...Ch. 2.6 - Inventory Control A California distributor of...Ch. 2.6 - Economic Lot Size The Great American Tire Co....Ch. 2.6 - Prob. 7ECh. 2.6 - Prob. 8ECh. 2.6 - Prob. 9ECh. 2.6 - Prob. 10ECh. 2.6 - Area Starting with a 100-foot-long stone wall, a...Ch. 2.6 - Prob. 12ECh. 2.6 - Length A rectangular corral of 54 square meters is...Ch. 2.6 - Refer to Exercise 13. If the cost of the fencing...Ch. 2.6 - Revenue Shakespeares Pizza sells 1000 large vegi...Ch. 2.6 - Prob. 16ECh. 2.6 - Cost A storage shed is to be built in the shape of...Ch. 2.6 - Cost A supermarket is to be designed as a...Ch. 2.6 - Volume A certain airline requires that rectangular...Ch. 2.6 - Area An athletic field [Fig.8] consists of a...Ch. 2.6 - Volume An open rectangular box is to be...Ch. 2.6 - Volume A closed rectangular box is to be...Ch. 2.6 - Amount of Oxygen in a Lake Let f(t) be the amount...Ch. 2.6 - Prob. 24ECh. 2.6 - Area Consider a parabolic arch whose shape may be...Ch. 2.6 - Prob. 26ECh. 2.6 - Surface Area An open rectangular box of volume 400...Ch. 2.6 - If f(x) is defined on the interval 0x5 and f(x) is...Ch. 2.6 - Technology Exercises Volume A pizza box is formed...Ch. 2.6 - Technology Exercises Consumption of Coffee in the...Ch. 2.7 - Prob. 1CYUCh. 2.7 - Rework Example 4 under the condition that the...Ch. 2.7 - On a certain route, a regional airline carries...Ch. 2.7 - Minimizing Marginal Cost Given the cost function...Ch. 2.7 - Minimizing Marginal Cost If a total cost function...Ch. 2.7 - Maximizing Revenue Cost The revenue function for a...Ch. 2.7 - Maximizing Revenue The revenue function for a...Ch. 2.7 - Cost and Profit A one-product firm estimates that...Ch. 2.7 - Maximizing Profit A small tie shop sells ties for...Ch. 2.7 - Demand and Revenue The demand equation for a...Ch. 2.7 - Maximizing Revenue The demand equation for a...Ch. 2.7 - Profit Some years ago, it was estimated that the...Ch. 2.7 - Maximizing Area Consider a rectangle in the xy-...Ch. 2.7 - Demand, Revenue, and Profit Until recently...Ch. 2.7 - Demand and Revenue The average ticket price for a...Ch. 2.7 - Demand and Revenue An artist is planning to sell...Ch. 2.7 - Demand and Revenue A swimming club offers...Ch. 2.7 - Prob. 15ECh. 2.7 - Prob. 16ECh. 2.7 - Price Setting The monthly demand equation for an...Ch. 2.7 - Taxes, Profit, and Revenue The demand equation for...Ch. 2.7 - Interest Rate A savings and loan association...Ch. 2.7 - Prob. 20ECh. 2.7 - Revenue The revenue for a manufacturer is R(x)...Ch. 2.7 - Prob. 22ECh. 2 - State as many terms used to describe graphs of...Ch. 2 - What is the difference between having a relative...Ch. 2 - Give three characterizations of what it means for...Ch. 2 - What does it mean to say that the graph of f(x)...Ch. 2 - Prob. 5FCCECh. 2 - Prob. 6FCCECh. 2 - Prob. 7FCCECh. 2 - Prob. 8FCCECh. 2 - Prob. 9FCCECh. 2 - Prob. 10FCCECh. 2 - Prob. 11FCCECh. 2 - Prob. 12FCCECh. 2 - Prob. 13FCCECh. 2 - Prob. 14FCCECh. 2 - Outline the procedure for solving an optimization...Ch. 2 - Prob. 16FCCECh. 2 - Figure (1) contains the graph of f(x), the...Ch. 2 - Figure (2) shows the graph of function f(x) and...Ch. 2 - In Exercise 36, draw the graph of a function f(x)...Ch. 2 - In Exercise 36, draw the graph of a function f(x)...Ch. 2 - In Exercise 36, draw the graph of a function f(x)...Ch. 2 - In Exercise 36, draw the graph of a function f(x)...Ch. 2 - Exercise 712, refer to the graph in Fig. 3. List...Ch. 2 - Exercise 712, refer to the graph in Fig. 3. List...Ch. 2 - Exercise 712, refer to the graph in Fig. 3. List...Ch. 2 - Exercise 712, refer to the graph in Fig. 3. List...Ch. 2 - Exercise 712, refer to the graph in Fig. 3. List...Ch. 2 - Exercise 712, refer to the graph in Fig. 3. List...Ch. 2 - Properties of various functions are described...Ch. 2 - Properties of various functions are described...Ch. 2 - Properties of various functions are described...Ch. 2 - Properties of various functions are described...Ch. 2 - Properties of various functions are described...Ch. 2 - Properties of various functions are described...Ch. 2 - Properties of various functions are described...Ch. 2 - Prob. 20RECh. 2 - In Fig. 4 (a) and 4 (b), the t axis represents...Ch. 2 - U.S. Electric Energy United States electrical...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following parabolas. Include there x...Ch. 2 - Sketch the following curves. y=2x3+3x2+1Ch. 2 - Sketch the following curves. y=x332x26xCh. 2 - Sketch the following curves. y=x33x2+3x2Ch. 2 - Sketch the following curves. y=100+36x6x2x3Ch. 2 - Sketch the following curves. y=113+3xx213x3Ch. 2 - Sketch the following curves. y=x33x29x+7Ch. 2 - Sketch the following curves. y=13x32x25xCh. 2 - Sketch the following curves. y=x36x215x+50Ch. 2 - Sketch the following curves. y=x42x2Ch. 2 - Sketch the following curves. y=x44x3Ch. 2 - Sketch the following curves. y=x5+20x+3(x0)Ch. 2 - Sketch the following curves. y=12x+2x+1(x0)Ch. 2 - Let f(x)=(x2+2)3/2. Show that the graph of f(x)...Ch. 2 - Show that the function f(x)=(2x2+3)3/2 is...Ch. 2 - Let f(x) be a function whose derivative is...Ch. 2 - Let f(x) be a function whose derivative is...Ch. 2 - Position Velocity and Acceleration A car traveling...Ch. 2 - The water level in a reservoir varies during the...Ch. 2 - Population near New York City Let f(x) be the...Ch. 2 - For what x does the function f(x)=14x2x+2,0x8,...Ch. 2 - Find the maximum value of the function...Ch. 2 - Find the minimum value of the function...Ch. 2 - Surface Area An open rectangular box is to be 4...Ch. 2 - Volume A closed rectangular box with a square base...Ch. 2 - Volume A long rectangular sheet of metal 30 inches...Ch. 2 - Maximizing the Total Yield A small orchard yields...Ch. 2 - Inventory Control A publishing company sells...Ch. 2 - Profit if the demand equation for a monopolist is...Ch. 2 - Minimizing time Jane wants to drive her tractor...Ch. 2 - Maximizing Revenue A travel agency offers a boat...
Additional Math Textbook Solutions
Find more solutions based on key concepts
First Derivative Test a. Locale the critical points of f. b. Use the First Derivative Test to locale the local ...
Calculus: Early Transcendentals (2nd Edition)
For Problems 23-28, write in simpler form, as in Example 4. logbFG
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
1. How is a sample related to a population?
Elementary Statistics: Picturing the World (7th Edition)
Check Your Understanding
Reading Check Complete each sentence using > or < for □.
RC1. 3 dm □ 3 dam
Basic College Mathematics
Teacher Salaries
The following data from several years ago represent salaries (in dollars) from a school distri...
Elementary Statistics: A Step By Step Approach
Find all solutions of each equation in the interval .
Precalculus: A Unit Circle Approach (3rd Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Find the minimum cost of a rectangular box of volume 120 cm³ whose top and bottom cost 6 cents per cm² and whose sides cost 5 cents per cm². Round your answer to nearest whole number cents. Cost = cents.arrow_forwardFind the absolute extrema of the function f(x, y) = x² + y² - 3x-3y+3 on the domain defined by x² + y² <9. Round answers to 3 decimals or more. Absolute Maximum: Absolute Minimum:arrow_forwardFind the maximum and minimum values of the function f(x, y) = e² subject to ï³ + y³ = 128 Please show your answers to at least 4 decimal places. Enter DNE if the value does not exist. Maximum value:arrow_forward
- A chemical manufacturing plant can produce x units of chemical Z given p units of chemical P and 7 units of chemical R, where: z = 140p0.6,0.4 Chemical P costs $300 a unit and chemical R costs $1,500 a unit. The company wants to produce as many units of chemical Z as possible with a total budget of $187,500. A) How many units each chemical (P and R) should be "purchased" to maximize production of chemical Z subject to the budgetary constraint? Units of chemical P, p = Units of chemical R, r = B) What is the maximum number of units of chemical Z under the given budgetary conditions? (Round your answer to the nearest whole unit.) Max production, z= unitsarrow_forwardA firm manufactures a commodity at two different factories, Factory X and Factory Y. The total cost (in dollars) of manufacturing depends on the quantities, and y produced at each factory, respectively, and is expressed by the joint cost function: C(x, y) = x² + xy +4y²+400 A) If the company's objective is to produce 1,900 units per month while minimizing the total monthly cost of production, how many units should be produced at each factory? (Round your answer to whole units, i.e. no decimal places.) To minimize costs, the company should produce: units at Factory X and units at Factory Y B) For this combination of units, their minimal costs will be enter any commas in your answer.) Question Help: Video dollars. (Do notarrow_forwarduse Lagrange multipliers to solvearrow_forward
- Suppose a Cobb-Douglas Production function is given by the following: P(L,K)=80L0.75 K-0.25 where L is units of labor, K is units of capital, and P(L, K) is total units that can be produced with this labor/capital combination. Suppose each unit of labor costs $400 and each unit of capital costs $1,600. Further suppose a total of $384,000 is available to be invested in labor and capital (combined). A) How many units of labor and capital should be "purchased" to maximize production subject to your budgetary constraint? Units of labor, L = Units of capital, K = B) What is the maximum number of units of production under the given budgetary conditions? (Round your answer to the nearest whole unit.) Max production = unitsarrow_forwardSuppose a Cobb-Douglas Production function is given by the function: P(L, K) = 7L0.0 K0.4 Furthemore, the cost function for a facility is given by the function: C(L, K) = 100L +400K Suppose the monthly production goal of this facility is to produce 15,000 items. In this problem, we will assume L represents units of labor invested and K represents units of capital invested, and that you can invest in tenths of units for each of these. What allocation of labor and capital will minimize total production Costs? Units of Labor L = Units of Capital K = (Show your answer is exactly 1 decimal place) (Show your answer is exactly 1 decimal place) Also, what is the minimal cost to produce 15,000 units? (Use your rounded values for L and K from above to answer this question.) The minimal cost to produce 15,000 units is $ Hint: 1. Your constraint equation involves the Cobb Douglas Production function, not the Cost function. 2. When finding a relationship between L and K in your system of equations,…arrow_forwardFind the absolute maximum and minimum of f(x, y) = x + y within the domain x² + y² ≤ 4. Please show your answers to at least 4 decimal places. Enter DNE if the value does not exist. 1. Absolute minimum of f(x, y) isarrow_forward
- Suppose that one factory inputs its goods from two different plants, A and B, with different costs, 3 and 7 each respective. And suppose the price function in the market is decided as p(x, y) = 100 - x - y where I and y are the demand functions and 0 < x,y. Then as x = y = the factory can attain the maximum profit,arrow_forwardEvaluate the following integrals, showing all your workingarrow_forwardConsider the function f(x) = 2x³-4x2-x+1. (a) Without doing a sketch, show that the cubic equation has at least one solution on the interval [0,1]. Use a theorem discussed in lectures, or see Section 1.8 of Calculus (7th ed) by Stewart. Ensure that the conditions of the theorem are satisfied (include this in your solution) (b) Now, by sketching the cubic (by hand or by computer), you should see that there is, in fact, exactly one zero in the interval [0,1]. Use Newton's method to find this zero accurate to 3 decimal places. You should include a sketch of the cubic, Newton's iteration formula, and the list of iterates. [Use a computer if possible, e.g., a spreadsheet or MatLab.]arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Finding Local Maxima and Minima by Differentiation; Author: Professor Dave Explains;https://www.youtube.com/watch?v=pvLj1s7SOtk;License: Standard YouTube License, CC-BY