EBK ENGINEERING MECHANICS
15th Edition
ISBN: 9780137569830
Author: HIBBELER
Publisher: VST
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 22, Problem 41P
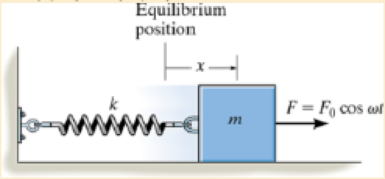
If the block-and-spring model is subjected to the periodic force F=F0 cos ωt, show that the differential equation of motion is ẍ + (k/m)x = (F0/m) cos ωt , where x is measured from the equilibrium position of the block. What is the general solution of this equation?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Find the equation of motion of the following spring system.
Consider a mass-spring system shown below.
X1
m
k₁
ooooo
The system model is given by
d²x
m
m₁
1 d1²
dx,
2 di²
1
· + (k₁₂ + k₂) x ₂ −k ₂x₂=F₁ (1)
1
k₂
ooooo
F₁
k₂x₂ + (k₂ + k ₂) x₂ = F₂(t)
k₂ +k z
2
m_s
(m_s²³ + k₁+k₂
²+k₁ + k ₂ ) ( m ₂s ² + k₂ + k ₂) -k
2
where F₁(t) and F₂(t) are the inputs to the system. Find the transfer function X₁(s)/F₁(s).
k ₂
(m₁s²+k₁+k₂) (m₂s² + k ₂2 +k₂ ) − k²/
2
₁s² + k ₁+k₂)
1
(m₂x²+₁+k₂) (m₂x²+k₂+^₂)=R}
2 ) ( m²₂ s² + k₂ + k ₂
1
2
m₂
k ₁+k₂
1
(m₁s²+k₁ + k₂) (m₂s² + k₂ + k 3) − k ²/
k 3
(m₂x²+k₂+k₂) (m₂x²+k₂+k₂) −R}
k ²
(m₂s² + k ₂+k₂)
(m₂x²+k₂ +k₂) (m₂x²+k₂+A₂)-R²
3)
k3
ooooo
F₂
Derive the equation of motion of the system shown in the figure below,
using the Newton's second law of motion.
k1
k2
m
Linear mass-spring system
Chapter 22 Solutions
EBK ENGINEERING MECHANICS
Ch. 22 - A spring is stretched 175 mm by an 8-kg block. If...Ch. 22 - A spring has a stiffness of 800 N/m. If a 2-kg...Ch. 22 - Prob. 3PCh. 22 - Prob. 4PCh. 22 - Prob. 5PCh. 22 - Prob. 6PCh. 22 - Prob. 7PCh. 22 - Prob. 8PCh. 22 - A 3-kg block is suspended from a spring having a...Ch. 22 - Prob. 10P
Ch. 22 - Prob. 13PCh. 22 - Prob. 14PCh. 22 - Prob. 16PCh. 22 - Prob. 17PCh. 22 - A uniform board is supported on two wheels which...Ch. 22 - Prob. 24PCh. 22 - Prob. 30PCh. 22 - Prob. 31PCh. 22 - Prob. 32PCh. 22 - Determine the differential equation of motion of...Ch. 22 - Prob. 36PCh. 22 - If the block-and-spring model is subjected to the...Ch. 22 - A block which has a mass m is suspended from a...Ch. 22 - A 4-lb weight is attached to a spring having a...Ch. 22 - A 4-kg block is suspended from a spring that has a...Ch. 22 - A 5-kg block is suspended from a spring having a...Ch. 22 - Prob. 48PCh. 22 - The light elastic rod supports a 4-kg sphere. When...Ch. 22 - Find the differential equation for small...Ch. 22 - Prob. 52PCh. 22 - The fan has a mass of 25 kg and is fixed to the...Ch. 22 - In Prob. 22-53 , determine the amplitude of...Ch. 22 - Prob. 55PCh. 22 - Prob. 56PCh. 22 - Prob. 57PCh. 22 - Prob. 58PCh. 22 - Prob. 59PCh. 22 - Prob. 60PCh. 22 - Prob. 61PCh. 22 - Prob. 62PCh. 22 - Prob. 65PCh. 22 - Determine the magnification factor of the block,...Ch. 22 - Prob. 67PCh. 22 - The 200-lb electric motor is fastened to the...Ch. 22 - Prob. 70PCh. 22 - Prob. 72PCh. 22 - Prob. 73PCh. 22 - Prob. 74PCh. 22 - Prob. 75PCh. 22 - Prob. 76PCh. 22 - Prob. 79P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Consider the following equation of motion that describes the dynamics of a particle subjected to a gravitational field and restricted to the surface of a cone i +rở² sin (a)² + g cos (a) sin (a) Using the equation of motion, determine the dynamics for small oscillations around the equilibrium point. Consider that ở = . Specify the frequency of oscillation, the balance point and its stability. mr²arrow_forwardPlease show the complete solution.arrow_forwardWhich of the following cannot be the position of the mass of a mass-spring system: Ox (t) = 5.5 cos 8t O x (t) = 5 e 2t cos 7t Ox (t) = 1.25 sin(11t+2) Ox (t) = 3 cos 2t + 7 sin 2tarrow_forward
- Determine the equivalent spring constant of the system shown in the figure.arrow_forwardI need the answer as soon as possiblearrow_forwardIf both springs are usntretched when the mass is in the central position shown, determine the static deflection of the mass. What is the period of oscillatory motion about the position of static equilibrium? The mass m = 3.4, the spring constant k = 295 N/m, and the angle theta = 31 degreesarrow_forward
- e(+) 3r S.E.P. The homogeneous disc with a mass of 4m and radius of 3r is supported at point 0. For small oscillations, find the equations of motion of the two – degree – of – freedom system in terms of the given parameters (k,m,r), and show them in the matrix form. The system is in the static equilibrium position at the instant given. 4m 3 2k Sm Ta(+) 5k Зт wwarrow_forwardSHOW YOUR STEP BY STEP SOLUTION. 1. Assuming that the displacement (x) resulting from the application of a force F at a point A is small, find the equivalent spring constant of the system that relates the applied force F to the displacement x. k- 2karrow_forwardDetermine the equivalent spring stiffness of the system using the displacement of the block as the generalized coordinate E = 200 x 10" N/m2 I = 1.6 x 10°m* 6 x 10 N/m 3 m- 2 x 10° N/m m 3 x 10' N/m 5 x 10° N/marrow_forward
- Mechanical Vibrationsarrow_forwardThe following mass-and-spring system has stiffness matrix K. The system is set in motion from rest (x, '(0) = x2'(0) = 0) in its equilibrium position (x, (0) = x2(0) = 0) with the given external forces F, (t) = 0 and F, (t) = 270 cos 4t acting on the masses m, and m,, respectively. Find the resulting motion of the system and describe it as a %3D superposition of oscillations at three different frequencies. k2 mi ww m2 k3 - (k, + k2) k2 K= k2 - (k2 + k3) m, = 1, m, = 2; k, = 1, k, = 6, k3 = 2 %3D Find the resulting motion of the system. X4 (t) = X2(t) (Type exact answers, using radicals as needed.)arrow_forwardThe 10 N cylinder moves in a frictionless pipe. Spring constants are k1 = 150 N / m and k2 = 200 N / m. When the system is at rest, d = 0.5 m. (d is the distance from the right end of the arc k2). The system rotates around a fixed z-axis. Find the constant velocity of the cylinder for d = 0.20 m?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...
Mechanical Engineering
ISBN:9781305501607
Author:Andrew Pytel And Jaan Kiusalaas
Publisher:CENGAGE L
Ch 2 - 2.2.2 Forced Undamped Oscillation; Author: Benjamin Drew;https://www.youtube.com/watch?v=6Tb7Rx-bCWE;License: Standard youtube license