Numerical Methods for Engineers
7th Edition
ISBN: 9780073397924
Author: Steven C. Chapra Dr., Raymond P. Canale
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 2, Problem 1P
Write pseudocode to implement the flowchart depicted in Fig. P2.1. Make sure that proper indentation is included to make the structure clear.
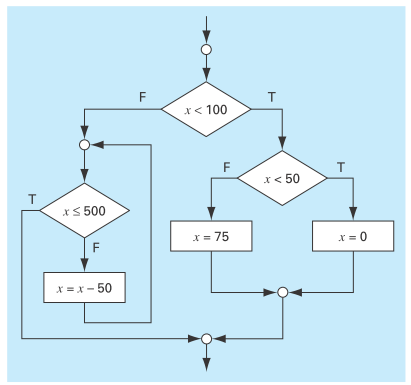
FIGURE P2.1
Expert Solution & Answer
To determine
The pseudo code for the flow chart provided flowchart.
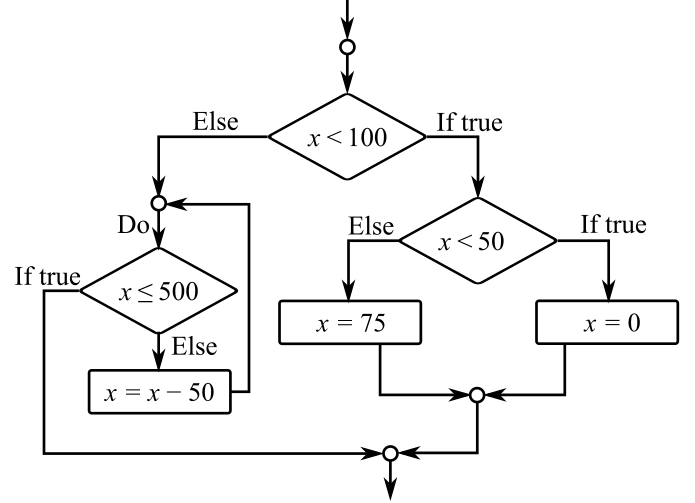
Answer to Problem 1P
Solution:
The pseudo codeto the provided question is as follows:
IF x < 100 THEN
IF x < 50 THEN
x = 0
ELSE
x = 75
END IF
ELSE
DO
IF x <= 500 EXIT
x = x - 50
END DO
ENDIF
Explanation of Solution
Given:
The flow chart is as follows:
The flow chart,
The pseudo code to the provided question is as follows:
IF x < 100 THEN
IF x < 50 THEN
x = 0
ELSE
x = 75
END IF
ELSE
DO
IF x <= 500 EXIT
x = x - 50
END DO
ENDIF
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
7. Show that for R sufficiently large, the polynomial P(z) in Example 3, Sec. 5, satisfies
the inequality
|P(z)| R.
Suggestion: Observe that there is a positive number R such that the modulus of
each quotient in inequality (9), Sec. 5, is less than |an|/n when |z| > R.
9. Establish the identity
1-
1+z+z² +
2n+1
...
+z" =
1- z
(z1)
and then use it to derive Lagrange's trigonometric identity:
1
1+ cos cos 20 +... + cos no =
+
2
sin[(2n+1)0/2]
2 sin(0/2)
(0 < 0 < 2л).
Suggestion: As for the first identity, write S = 1+z+z² +...+z" and consider
the difference S - zS. To derive the second identity, write z =
eie in the first one.
8. Prove that two nonzero complex numbers z₁ and Z2 have the same moduli if and only if
there are complex numbers c₁ and c₂ such that Z₁ = c₁C2 and Z2 = c1c2.
Suggestion: Note that
(i≤
exp (101+0) exp (01-02)
and [see Exercise 2(b)]
2
02
Ꮎ
-
= = exp(i01)
exp(101+0) exp (i 01 - 02 ) = exp(102).
i
2
2
Chapter 2 Solutions
Numerical Methods for Engineers
Ch. 2 - 2.1 Write pseudocode to implement the flowchart...Ch. 2 - Prob. 2PCh. 2 - 2.3 Develop, debug, and document a program to...Ch. 2 - The sine function can be evaluated by the...Ch. 2 - 2.5 Develop, debug, and document a program for...Ch. 2 - The following algorithm is designed to determine a...Ch. 2 - The divide and average method, an old-time method...Ch. 2 - 2.8 An amount of money P is invested in an account...Ch. 2 - 2.9 Economic formulas are available to compute...Ch. 2 - 2.10 The average daily temperature for an area can...
Ch. 2 - Develop, debug, and test a program in either a...Ch. 2 - 2.12 The bubble sort is an inefficient, but...Ch. 2 - Figure P2.13 shows a cylindrical tank with a...Ch. 2 - 2.14 Two distances are required to specify the...Ch. 2 - Develop a well-structured function procedure that...Ch. 2 - Prob. 16PCh. 2 - Develop well-structured programs to (a) determine...Ch. 2 - 2.18 Piecewise functions are sometimes useful when...Ch. 2 - Develop a well-structured function to determine...Ch. 2 - 2.20 Develop a well-structured function to...Ch. 2 - 2.21 Manning’s equation can be used to compute the...Ch. 2 - 2.22 A simply supported beam is loaded as shown in...Ch. 2 - ThevolumeV of liquid in ahollow horizontal...Ch. 2 - 2.24 Develop a well-structured program to compute...Ch. 2 - The pseudocode in Fig. P2.25 computes the...Ch. 2 - 2.26 The height of a small rocket y can be...Ch. 2 - 2.27 As depicted in Fig. P2.27, a water tank...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- 1) Compute the inverse of the following matrix. 0 1 1 A = 5 1 -1 2-3 -3arrow_forward2) Consider the matrix M = [1 2 3 4 5 0 2 3 4 5 00345 0 0 0 4 5 0 0 0 0 5 Determine whether the following statements are True or False. A) M is invertible. B) If R5 and Mx = x, then x = 0. C) The last row of M² is [0 0 0 0 25]. D) M can be transformed into the 5 × 5 identity matrix by a sequence of elementary row operations. E) det (M) 120 =arrow_forward3) Find an equation of the plane containing (0,0,0) and perpendicular to the line of intersection of the planes x + y + z = 3 and x y + z = 5. -arrow_forward
- 1) In the xy-plane, what type of conic section is given by the equation - √√√(x − 1)² + (y − 1)² + √√√(x + 1)² + (y + 1)² : - = 3?arrow_forward3) Let V be the vector space of all functions f: RR. Prove that each W below is a subspace of V. A) W={f|f(1) = 0} B) W = {f|f(1) = ƒ(3)} C) W={ff(x) = − f(x)}arrow_forwardTranslate the angument into symbole from Then determine whether the argument is valid or Invalid. You may use a truth table of, it applicable compare the argument’s symbolic form to a standard valid or invalid form. pot out of bed. The morning I did not get out of bed This moring Mat woke up. (1) Cidt the icon to view tables of standard vald and braild forms of arguments. Let prepresent."The morning Must woke up "and let a represent “This morning I got out of bed.” Seled the cared choice below and II in the answer ber with the symbolic form of the argument (Type the terms of your expression in the same order as they appear in the original expression) A. The argument is valid In symbolic form the argument is $\square $ B. The angunent is braid In symbolic form the argument is $\square $arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY