
Sketching a Vector Field In Exercises 1 and 2, find
To calculate:
Answer to Problem 1RE
Solution:
Explanation of Solution
Given:
Formula used:
Calculation:
Using (1), the magnitude of a vector function
The divergence of a vector field
We start by making a table showing the vector field at several points. The table shown is a
small sample. The vector field lines at many other points should be calculated to get a
representative vector field, which can be obtained by using a computer algebra system.
| x | -2 | -1 | 0 | 0 | 1 | 2 |
| y | 1 | -1 | -1 | 1 | -1 | -1 |
| z | 1 | 1 | 1 | 1 | 1 | 1 |
Next, we draw line segments at the points to represent the vector field
The sketch of the representative vectors, is shown below
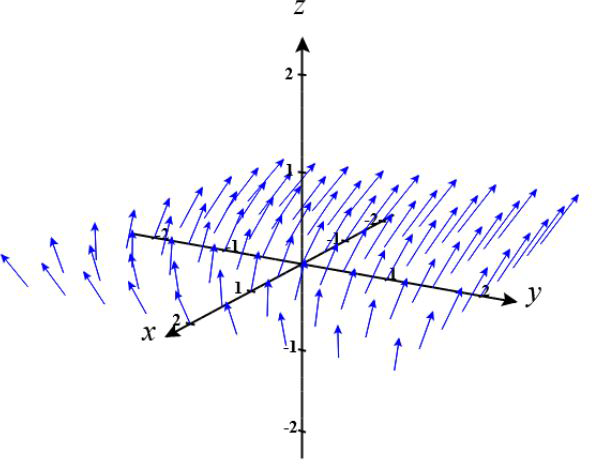
Interpretation: The vector field is irrotational in nature and has a positive divergence
Want to see more full solutions like this?
Chapter 15 Solutions
Multivariable Calculus
- Explain the key points and reasons for the establishment of 12.3.2(integral Test)arrow_forwardUse 12.4.2 to determine whether the infinite series on the right side of equation 12.6.5, 12.6.6 and 12.6.7 converges for every real number x.arrow_forwarduse Cauchy Mean-Value Theorem to derive Corollary 12.6.2, and then derive 12.6.3arrow_forward
- Explain the focus and reasons for establishment of 12.5.1(lim(n->infinite) and sigma of k=0 to n)arrow_forwardExplain the focus and reasons for establishment of 12.5.3 about alternating series. and explain the reason why (sigma k=1 to infinite)(-1)k+1/k = 1/1 - 1/2 + 1/3 - 1/4 + .... converges.arrow_forwardExplain the key points and reasons for the establishment of 12.3.2(integral Test)arrow_forward
- Use identity (1+x+x2+...+xn)*(1-x)=1-xn+1 to derive the result of 12.2.2. Please notice that identity doesn't work when x=1.arrow_forwardExplain the key points and reasons for the establishment of 11.3.2(integral Test)arrow_forwardTo explain how to view "Infinite Series" from "Infinite Sequence"’s perspective, refer to 12.2.1arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning


